This is a 17-games-in-one collaborative cart. There have been a couple of 16-in-1 jams done before but these tended to be presented as 16 standalone games with a menu screen to pick between them. I wanted to do something that was an homage to Lazy Jones on the C64 (https://www.youtube.com/watch?v=Y7DyoDJCqac), where you have 16 mini-games but also an overarching 17th game that ties them all together.
There were 16 different developers in 10 countries: UK, USA, Canada, Australia, France, Russia, Hungary, Norway, Finland, Sweden.
Contributors were: @Liquidream @platformalist @p01 @gruber_music @egordorichev @brintown @enargy @viza @MrHodgepants @kometbomb @johanpeitz @2darray @GregosEl @dollarone, plus UncleSporky and... me!
Fly around space collecting crystals to open “anomalies”. Each one will send you to another dimension where a weird challenge will present itself. Do well and your ship will be refuelled accordingly! Try to get through all 16 anomalies before you run out of fuel.









Hey all, it's been a while (having kids) but we are back on with our mission to get 17 games (16 plus an overarching meta-game to tie them all together) in one collab cart.
We are currently at 6 or 7 games and I'm going to give this one final push to see if we can finish it!
Join us for full rules and discussion here:
Hi all,
Now that family stuff is a bit more under control, I want to fire this up again! I've got limited availability but I'll do my best to give prompt replies. If in doubt, stick to the guidelines below.
Let's make a 17-in-1 cart of minigames! 16 games plus an over-arching "meta" game to tie them all together, give the player a "final score" etc.
I've built a space-themed meta-game already (see below). I'm looking for people to make some minigames for the player to explore. The first 16 (serious and functional) submissions that conform the the rules will be added to the cart.
Please read the rules fully before submitting your game. I'm flexible to a certain extent but please check with me first!
Games finished so far: 6 of 17
Some links:
Discord: https://discord.gg/rncwcsR
Twitter hashtag is #17in1jam
List of resources currently being used: https://www.dropbox.com/s/fbx8x01bvg2g3z8/17-in-1%20memory%20usage.xlsx?dl=0
Help with reducing tokens: https://github.com/seleb/PICO-8-Token-Optimizations
Help with reducing characters: https://pastebin.com/MVhr16td



EDIT: This is now postponed while baby is incoming. I'll try my hardest to pick this up in the future but it's not likely to be until at least late 2018. I'm aware that @enargy and @pingo had games in progress, bringing the total potentially to 9. There were also a few others who expressed interest, and I'll probably do one or two more eventually.
If you've already posted a game, thanks for your contribution, and please feel free to withdraw your game if you don't fancy waiting.
Old post begins here:
Let's make a cart of minigames!
Games finished: 6 of 17
Discord: https://discord.gg/rncwcsR
Twitter hashtag is #17in1jam
Resources being used: https://www.dropbox.com/s/oca0s4bsr7pe6dp/17-in-1%20memory%20usage.xlsx?dl=0
Help with reducing tokens: https://github.com/seleb/PICO-8-Token-Optimizations
Help with reducing characters: https://pastebin.com/MVhr16td
Totally been done before (see @josefnpat's carts here). But we should try 16 minigames plus an over-arching "meta" game to tie them all together, give the player a "final score" etc.








Happy New Year all!
Please excuse my ignorance and do stop me if this has all been done before.
I'm thinking of bringing together a large collaborative game for Pico-8, based on the concept used in Lazy Jones for the C64:
https://www.c64-wiki.com/wiki/Lazy_Jones
https://www.youtube.com/watch?v=Y7DyoDJCqac
Basically Lazy Jones was the first example I know of, of a game that features lots of minigames (18 I think). In Lazy Jones, you walk round a hotel avoiding enemies etc, and opening doors, and behind each door is a timed minigame. The aim of the game was to play all of the games and get the highest total score.
I wouldn't be looking to replicate Lazy Jones exactly, rather it would use the same general idea - an overarching "meta" game with as many minigames as possible. Naturally I'd be looking for the different games to come from you guys!
Done on the C64 this was quite the technical feat, but done on the Pico-8 with all the Tweetjam skillz I've seen on here, this could be awesome. We only have half as much RAM available, but a lot of the C64 code would have been hardware stuff that is handled automatically by the Pico-8, so maybe a fairly level playing field?
In order to try to get as many games as possible we'd have to impose a few restrictions (yay!):
> Maybe some kind of token/char limit - we'd need to strike the right balance between number of games and the scope of those games.
> Each game has some kind of final score and some kind of timer/lives system, to feed into the "meta" score.
> Screen space restrictions, to allow for general HUD stuff etc.
> Light on sprites and SFX usage - maybe share assets between games or come up with a master asset list for all games and try to optimise?
> Global music same for all games, maybe each game can decide to play it or not.
Obviously this is all very early ideas, and I'd very much welcome feedback - and as much help as possible - in shaping the final thing!
Let me know what you think :)
Neil



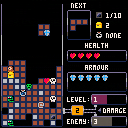
A mixture of two genres – a Roguelike and a Tetris-style game – based on a prototype I made with a friend (@ollie_read) in 8 hours during a "Crafts and Gin" Game Jam back in 2012.
• 10 levels
• Procedural generation
• Musicality!
• Old-school gameplay
• But actually winnable though
Arrow keys to move/rotate/drop blocks, X + arrows to move rogue and fight monsters.
Full instructions can be found in game. I hope you enjoy it.
Thoughts
This version of the game took a long time to make – more than 40 coding sessions during evenings/weekends of July-November 2017. I had the core game fully working within a few sessions, and the rest has literally been set dressing and "polish" (it still looks like programmer art!). Presentation is quite pompous in places, e.g. a full menu system; this is simply because I wanted to make the game as "finished" as possible (I teach game dev so I want to set a good example).
In order to fit the standard 10x20 grid (plus 4 invisible rows for spawning blocks) on the screen, I had to use 6x6 pixel sprites for each cell rather than the easier option of a map of 8x8 pixel cells. Making clear pixel art in 6x6 tiles is hard, but I’m quite happy with the monster designs and animations – I think they have personality.
This was my first Pico-8 / Lua game so wasn’t sure how restrictive the CPU or token/char count would be in practice. I was worried it would struggle with drawing so many sprites but seems okay? (stat() was showing about 10% CPU at worst). Token budget was more than enough too, but I only realised this once I had carefully implemented most of the critical content – so in general the code is unnecessarily dense. I was disappointed at first that it would easily fit into the restrictions, but then I noticed that I’d gone well over the limit for the compressed .p8.png format, which added a nice little challenge towards the end. Had two runs at crunching - the first involved me hard-coding a load of values and adding short function references, but this meant that I would have to retest the entire game thoroughly to check I hadn't broken anything, so instead I rolled back and just minimised the comments :)
A warning for beginners: Tetris clones might seem like an ideal "basic" project to work on, but I found there are lots of unforeseeable logic problems/exceptions, and quite a few subtle UX tricks that you have to do to make the game "feel" right (some I've done, some I haven't). So beware, I guess.
I’ve got it so the music is in sync with the GFX, but I have had to implement procedural music in order to do this. Originally I had a song that I played at a set tempo and synced up with the monsters "dancing", but if the Pico-8 loses focus (e.g. to desktop) the audio continues to play while the GFX freezes, so the music goes out of sync. Also noticed that pausing and unpausing the game seemed to cause the Pico-8 to throw the sync out by 2 ticks. In the end I created separate instruments as SFX and made my own "song" by triggering them on certain ticks. It’s no accident that the game follows a 12-bar blues pattern; finally my GCSE music lessons paid off.
With so much RNG it was hard to balance, especially while preserving the luck-factor of a roguelike. This meant that I had to complete several runs each time I changed something, to allow for fluctuations in RNG. The longer I've worked on it, the more I've lost all objective sense of how difficult it is, but it is definitely winnable. I hope you guys enjoy it anyway; do let me know how you get on.
Neil














 16 comments
16 comments