prof: CPU cycle counter

pancelor • 2022-01-11*2022-01-11 03:31* •

BBS>

PICO-8>Code Snippets

tl;dr

Run load #prof in the PICO-8 console, then edit the last tab with some code you want to measure:

prof(function(x)
  local _=sqrt(x)   -- code snippet 1
end,function(x)
  local _=x^0.5     -- code snippet 2
end,{ locals={9} }) -- "locals" (optional) are passed in as args

Run the cart: it will tell you exactly how many cycles it takes to run each code snippet.

what is this?

This tool measures precisely how many cycles it takes to run arbitrary snippets of code. I use it all the time when I'm trying to figure out the fastest way to write an algorithm. For example, it's massively helpful to know the fastest way to calculate abs(x) in a modular synthesizer that needs to run this operation tens of thousands of times per second.

For context, PICO-8 runs at 8 million cycles per second. This number is unimaginably large and yet also hundreds of times slower than most desktop computers. To keep things in perspective, I like to remember that 1400 cycles is equal to 1% of your CPU budget each frame (at 60 fps -- 8*1024*1024/60/100 = 1398.1)

The wiki lists cycle costs for individual operations, but I often prefer to directly compare two larger snippets of code against each other, so I built this cycle-counting tool. Plus, the wiki can get out of date but this tool will always remain accurate, since it actively measures speed instead of looking it up.

For the curious, here's how I'm able to mesaure exact cycle counts. Essentially, I run your code many times and compare it against running nothing many times, using stat(1) and stat(2) for timing:

how do I use it?

Run load #prof in the PICO-8 console, then edit the last tab.

The cart comes with detailed instructions, reproduced here for your convenience:

There are also instructions included on two alternate ways you can profile your code, without using prof:

demo

Here's an old demo program to wow you:

cyclecounter

by pancelor

Cart #cyclecounter-2 | 2022-01-16 | Code ▽ | Embed ▽ | License: CC4-BY-NC-SA

This is neat but impractical; for everyday usage, you'll want to load #prof and edit the last tab.

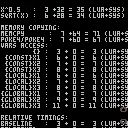
various results

Here are some speed comparisons I found interesting. Some of these may be out of date now, but they were interesting:

poke4 v. memcopy

prof(function() memcpy(0,0x200,64) end,       -- 71 (7 lua, 64 sys)
     function() poke4(0,peek4(0x200,16)) end) -- 67 (7 lua, 60 sys)

Copying 64 bytes of memory is very slightly faster if you use poke4 instead of memcpy -- interesting!
(iirc this is true for other data sizes... find out for yourself for sure by downloading and running the cart!)

edit: this has changed in 0.2.4b! the memcpy in this example now takes 39 cycles

constant folding

I thought lua code was not optimized by the Lua's bytecode compiler, but it turns out there are a few specific optimizations it will do.

prof(function() return 2+2 end,
     function() return 2+2+2+2+2+2+2+2 end)

These functions both take a single cycle! Lua apparently optimizes that long addition into a single instruction. @luchak found these explanations:

https://stackoverflow.com/questions/33991369/does-the-lua-compiler-optimize-local-vars/33995520
> Since Lua often compiles source code into byte code on the fly, it is designed to be a fast single-pass compiler. It does do some constant folding

A No Frills Introduction to Lua 5.1 VM Instructions (book)
> As of Lua 5.1, the parser and code generator can perform limited constant expression folding or evaluation. Constant folding only works for binary arithmetic operators and the unary minus operator (UNM, which will be covered next.) There is no equivalent optimization for relational, boolean or string operators.

constant folding...?

One further test case:

prof(function() local a=2  return 2+2+2+2+2+2+2+a end, --2
     function() local a=2  return a+2+2+2+2+2+2+2 end) --8

These cost different amounts! Constant-folding only seems to work at the start of expressions. (This is all highly impractical code anyway, but it's fun to dig in and figure out this sort of thing. Check out https://www.luac.nl/ too -- another fantastic tool to figure out this sort of thing.)