I'm struggling with a function that randomly picks up an element from a table with ponderated probability. For now this is my current code:
items = {
{value="a",probability=.35},
{value="b",probability=.35},
{value="c",probability=.145},
{value="d",probability=.145},
{value="e",probability=.008},
{value="f",probability=.002}
} -- total probability = 1
function rnd_item()
local rnd_number = rnd() -- between [0,0.99999)
local i = 1
local sum = items[i].probability
while sum < rnd_number do
i += 1
sum += items[i].probability
end
return items[i]
end |
What is the problem with the implementation? Right, In some cases it crashes because 'i' goes out of bounds. It seems that the problem occurs when rnd_number is near 1 (i.e. 0.99997) but I can't figure out how I fix it.
Is there a better implementation to solve the problem?

It looks like it's a decimal-to-binary conversion rounding error: when I run
numbers={.35,.35,.145,.145,.008,.002}
sum=0
for i=1,#numbers do
sum+=numbers[i]
print(tostr(numbers[i],true))
end
print(tostr(sum,true)) |
the numbers add up to 0x0.fffd < 0x0.ffff
I can think of three possible ways to handle it:
-
Instead of entering weights as decimal numbers, enter them as hexadecimal numbers with up to four hexadecimal places. This way, there's no rounding and therefore no rounding error, and you can ensure everything adds to 1.
- Enter the weights un-normalized (e.g. 350, 350, 145, 145, 8, 2), calculate the sum, and either:
2a. Normalize programmatically, dividing each weight but the last by the sum of the weights and setting the last to the remainder, or
2b. use
local rnd_number = rnd(sum) |
to generate a random number in the range [0, the sum).

+1 to everything packbat said, and +1 especially to method 2b. This is what I use:
function choose_weighted(opts)
-- given opts that looks like {
-- {ch_ground,3},
-- {ch_key,1},
-- {ch_ladder,6},
-- }, returns one of the first elements,
-- weighted based on the second elements
local sum=0
for e in all(opts) do
sum+=e[2]
end
if sum==0 then
return nil
end
local rng=rnd(sum)
for e in all(opts) do
rng-=e[2]
if rng<0 then
return e[1]
end
end
assert(false) --it should be impossible to execute this line
end |
some test code:
table={
{"x",20},
{".",2},
{"-",10},
}
cls()
s=""
for y=1,20 do
for x=1,20 do
s..=choose_weighted(table)
end
s..="\n"
end
print(s) |
result:
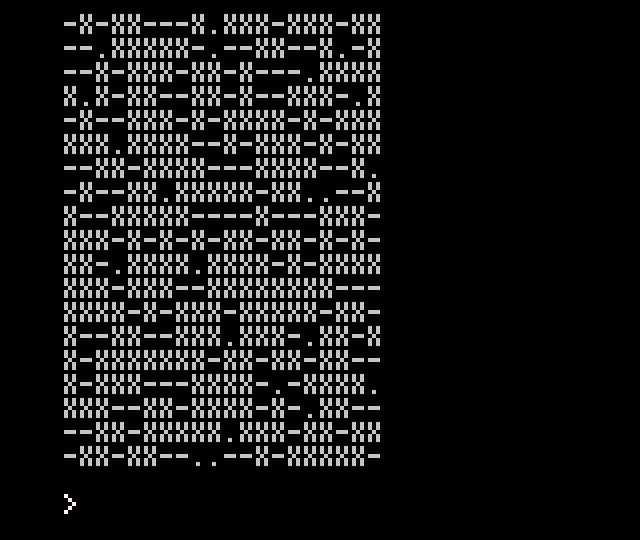

...actually, just realized there's a Method 3:
- Enter the weights unnormalized
- Run a calculation to replace weights in the table with cumulative sums
- Use the last entry in the table as the value for rnd(value) and just compare entry-by-entry each time you roll.
Or, alternatively, enter the normalized cumulative sums directly:
numbers={.35,.7,.845,.99,.998,1}
Edit: (not at computer, this is not tested)
items = { --cumulative probabilities
{value="a",probability=.35}, --.35
{value="b",probability=.7}, --.35
{value="c",probability=.845}, --.145
{value="d",probability=.99},--.145
{value="e",probability=.998},--.008
{value="f",probability=1}--.002
} -- total probability = 1
function rnd_item()
local rnd_number = rnd() -- between [0,0.99999)
for i=1,#items do
if items[i].probability > rnd_number then
return items[i] --will exit loop
end
end
end |
Edit 2: Did a Monte Carlo test in PICO-8 and it seems to be working just fine. Probably the best method from a tokens/CPU perspective - the rnd_item() function is 26 tokens and not a lot of cycles per function call (sorting the list from most likely to least likely as you did is optimal) - but a bit of a pain because you have to hand-calculate everything in advance and tweaking is inconvenient.

Yes, you hit the point. Method 3 is the best option despite you have to sort the items of the map.
Thanks man!

Not a man and you are welcome! It was a fun conundrum to try to disentangle - glad to be of service!

Here's a fast alternative, using a bag of tokens:
bag={}
function to_bag(e,n)
for i=1,n do
add(bag,e)
end
end
function from_bag()
return bag[1+rnd(#bag)\1]
end |
test code, borrowed from pancelor:
to_bag('x', 20)
to_bag('.', 2)
to_bag('-', 10)
cls()
s=""
for y=1,20 do
for x=1,20 do
s..= from_bag()
end
s..="\n"
end
print(s) |
this will use memory, depending on the granularity you need, but a hundred tokens is nothing and a thousand is still not much (any "big" thing you put in the bag is stored as a reference).
you could also shuffle the bag before use, and address the tokens in sequence. this way you can replay the same sequence if needed. also when you get to the end of the bag you're sure your tokens were uniformly distributed.

ooh clever @ ultrabrite! small token optimization: you can remove from_bag and instead call rnd(bag)


@packbat Oh shit, I'm sorry! Your avatar confused me...
@ultrabrite With your solution we've losing the weighted random selection. haven't we?

We already have "add(tbl, val, index)" so that rules out the "tbl, val, quantity" idea.

[Please log in to post a comment]









