This function allows the calculation of the distance between two points without squaring the numbers, greatly increasing the max distance before the number overflows.
function calc_dist(x1,y1,x2,y2) local xdif=x1-x2 local ydif=y1-y2 local atan=atan2(xdif,ydif) local xdist=cos(atan)*xdif local ydist=sin(atan)*ydif return xdist+ydist end |
it is also quite fast, doing 5000 calculations per frame (which is way more than you will ever need) uses around 0.63 CPU

If you don't need exact distances, @TetraPengwin, but still want to know how far away one sprite might be to another, this also works.
function calc_dist2(x1,y1,x2,y2) return abs(x1-x2)+abs(y1-y2) end |
Quite a bit faster and smaller.

Oh, BTW, @TetraPengwin. Is there a simple way to use the formula I have above where diagonal distances are not counted double as straight up and down ?
Here for instance is the formula I have in use:
x1=1, y1=1, x2=2, y2=1 - the distance would be 1.
However if x1=1, y1=1, x2=2, y2=2 - the distance would be 2, which is not entirely correct.

that's Tetra code or what Pythagora formula is for:
x1=1 y1=1 x2=2 y2=2 dx=x2-x1 dy=y2-y1 distance=sqrt(dx*dx+dy*dy) ?distance -- distance=1.4142 |

@dw817
That depends on what value you'd want to approximate the diagonals as instead. If a diagonal is approximated as a distance of 1, then you can just use max(abs(x1-2x),abs(y1-y2)), since in that case the smaller axis collapses into nothing. If an approximated diagonal is a distance of .7, then you can use
local dx,dy=abs(x1-x2),abs(y1-y2) return min(dx,dy)+.7*(max(dx,dy)-min(dx,dy)) |
That said, you're getting into the territory of grid-based movement, which makes more sense in games resembling board games rather than a continuous in-game space. That's an important distinction, as messing with approximations of diagonals means that you can't reliably use the same formulas for a continuous space.

Edit: This is incorrect. I forgot to consider if xdif or ydir equal 0 as pointed out in the comments below.
@TetraPengwin
You can get another (modest) speed boost out of your function if you want. Once you've calculated the angle with atan2 you don't need to calculate both the sin and the cos just one or the other.
function calc_dist(x1,y1,x2,y2)
local xdif=x1-x2
local ydif=y1-y2
local atan=atan2(xdif,ydif)
return xdif / cos(atan)
-- or this. both work:
-- return ydif / sin(atan)
end |
Even ignoring overflow issues, sqrt seems to be a real CPU hog on Pico-8 so it's not a terrible idea to avoid it when possible.

@jasondelaat
won’t work if xdiff or ydiff is zero
in such case, you need to take the max abs value, defeating the purpose

@freds72
Ah, oops! Not sure why I always forget to check edge cases like that but I do it all the time. Thanks for pointing it out it. Good reminder that I should check that what I'm saying is correct before I say it.

Good solution, @freds72 and @jasondelaat !
@kimiyoribaka, what you have is interesting and more what I am looking for.
Is there a way to count the # of pixels most efficiently reached between two points. Not A*Star, just a straight-line and it counts the pixels without having to write a FOR/END loop.
In this it would always be an integer value.
|
|
[8x8] |
For instance here it would be 7.

@dw817
That's approximating using a diagonal distance of 1. max(abs(y1-y2),abs(x1-x2)) should work.
@freds72
I don't see how that'd defeat the purpose. Wouldn't letting the function return early if either is 0 only make the function that much faster in edge cases? Even for the base version, I would think putting
if y1==y2 then return abs(x1-x2) end if x1==x2 then return abs(y1-y2) end |
would have a net benefit.

the equality test will only work for integers
for the more common case, you’ll need to pay the price of the max abs calls - hence my comment

Um...I'm confused? Why would that only work for integers? If those values aren't equal then the relevant other values won't be 0.
Also why are you concerned about max and abs? Those should be cheap functions. Max is just a simple comparison and in c no less. Abs is likely implemented by just setting some bits in easily predicted ways.

sure but the whole point was having a short & fast function to get distance.
function calls on pico are relatively costly (max costs more than twice a simple ‘if test )

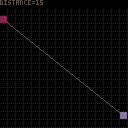
Hi @kimiyoribaka:
Here is your distance formula in use, and yep, that covers exactly what I want.
Thanks !!

Use arrow keys to navigate and ❎ to swap target control.

wow! this is pretty incredible. I spent some time sketching this to try and understand it, and eventually came up with this interactive diagram: https://www.desmos.com/geometry/o5krkiqx7g
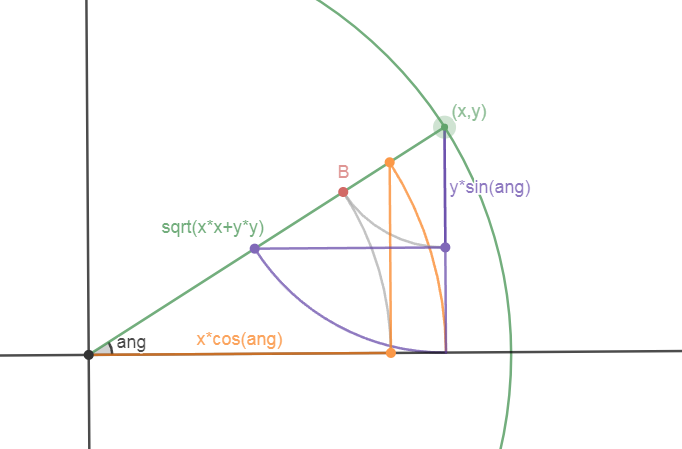
The surprising thing is that point B (where the two gray arcs meet the green line) is always one single point instead of two separate points. that's not something I forced to be true, it's just the result of this distance formula being correct. but why is it correct? this diagram doesn't really say, it just feels like magic.
I later figured out a nice proof, but that diagram is still satisfying so I wanted to show it off :)
a sketch of the proof:
- given a vector v, what's the dot product of v with its unit vector?
- the dot product
a dot bis given by either|a|*|b|*cos(ang)ora.x*b.x+a.y*b.y - by the first definition,
v dot v_unit = |v|*|v_unit|*cos(0) = |v|*|1|*1 = |v|. - but
v_unit=(cos(ang),sin(ang)), so by the second definition,v dot v_unit = v.x*v_unit.x+v.y*v_unit.y = x*cos(ang)+y*sin(ang). - the two definitions of dot product are equivalent, so
|v| = v dot v_unit = x*cos(ang)+y*sin(ang)∎

and here's a comparison of some different distance functions:
-- tokens: 15 -- cycles: 37 -- numerical issues: breaks down for differences in the hundreds. can cause big problems function dist_naive(dx,dy) return sqrt(dx*dx+dy*dy) end -- tokens: 39 -- cycles: 51 -- 54 (when "if" is hit) -- numerical issues: very slightly inaccurate; (5,12) is off by 0.0002 function dist_fancy(dx,dy) local u,v=abs(dx),abs(dy) if v < u then u,v=v,u end local a=u/v return v*sqrt(a*a+1) end -- tokens: 23 -- cycles: 21 -- numerical issues: very minor -- error in range (0,0)-(127,127): max 0.0017, avg 0.0004 (thanks, sparr!) function dist_trig(dx,dy) local ang=atan2(dx,dy) return dx*cos(ang)+dy*sin(ang) end -- tokens: 33 -- cycles: 26 -- 29 (when "if" is hit) -- numerical issues: slightly inaccurate; (5,12) is off by 0.0009 function dist_drakeblue(dx,dy) dx,dy=abs(dx),abs(dy) if dy < dx then dx,dy=dy,dx end return dy/sin(atan2(dx,dy)) end |
cycle counts were tested with prof(dist_naive,dist_fancy,dist_trig,dist_drakeblue,{locals={13,29}}).
also, check out this distance-comparison function. I haven't done the work to compare it properly, but it looks like another great option: https://www.lexaloffle.com/bbs/?pid=130349#p
Edit: here are some variations and speed analysis. Note that cycle counts are not directly comparable to dist_trig etc, because the less-than-check is part of the function
bonus: here's some code to show a fun visualization of the different methods. the black areas happen when sqrt() sees a negative number and returns zero

code:

I used this in PICO Space:
-- distance with trig -- to avoid too large numbers function dist_trig(a,b) local x,y=abs(b.x-a.x),abs(b.y-a.y) if x<y then x,y=y,x end -- accuracy goes down massively if x is much smaller than y return x/sin(atan2(y,x)) end |
The accuracy drop mentioned caused a very strange bug where the ship would spontaneously dive into the top and bottom of the sun. Turns out the game thought it was too close to the edge of the playing area (because of the bad distance value) and pushed it inwards - boom! It took quite some time to get to the bottom of that one.
I did some perf testing at the time and it's reasonably fast and I guess it's fairly "battle tested". I might see if I can find my test code and poke this and some of the other suggestions here some more since I'm thinking about updating that game anyway.

3d version for anyone interested:
-- overflow safe 3d vector length
-- faster than sqrt variant (23.5+14 vs. 27.5)
function v_len(v)
-- {x,y,z} format
local x,y,z=v[1],v[2],v[3]
-- {x=..,y=..,z=..} format
-- local x,y,z=v.x,v.y,v.z
-- token stressed version - adds 6 cycles to the mix
-- local x,y,z=unpack(v)
local ax=atan2(x,y)
local d2=x*cos(ax)+y*sin(ax)
local az=atan2(d2,z)
return d2*cos(az)+z*sin(az)
end
|
[Please log in to post a comment]




.jpeg)



