function arc(x, y, r, angle, c) if angle < 0 then return end for i = 0, .75, .25 do local a = angle if a < i then break end if a > i + .25 then a = i + .25 end local x1 = x + r * cos(i) local y1 = y + r * sin(i) local x2 = x + r * cos(a) local y2 = y + r * sin(a) local cx1 = min(x1, x2) local cx2 = max(x1, x2) local cy1 = min(y1, y2) local cy2 = max(y1, y2) clip(cx1, cy1, cx2 - cx1 + 2, cy2 - cy1 + 2) circ(x, y, r, c) clip() end end |
This function draws an arc by drawing a circle four times with different clipping regions.
Limitations:
- Can't draw a filled arc (but you can change the circ to a circfill for an interesting effect!)
- Can't set starting angle (but this would probably be easy to implement)

function arc(x, y, r, ang1, ang2, c) if ang1 < 0 or ang2 < 0 or ang1 >= 1 or ang2 > 1 then return end if ang1 > ang2 then arc(x, y, r, ang1, 1, c) arc(x, y, r, 0, ang2, c) return end for i = 0, .75, .25 do local a = ang1 local b = ang2 if a > i + .25 then goto next end if b < i then goto next end if a < i then a = i end if b > i + .25 then b = i + .25 end local x1 = x + r * cos(a) local y1 = y + r * sin(a) local x2 = x + r * cos(b) local y2 = y + r * sin(b) local cx1 = min(x1, x2) local cx2 = max(x1, x2) local cy1 = min(y1, y2) local cy2 = max(y1, y2) clip(cx1, cy1, cx2 - cx1 + 2, cy2 - cy1 + 2) circ(x, y, r, c) clip() ::next:: end end |
Here's a modification of that is able to draw an arc w/ any starting angle. Use ang1 as the start and ang2 as the end.

Ah, I was working on one of these myself recently, using clip() to select segments of circ() calls.
One thing I noted is that it's always possible to draw an arc with 3 or fewer calls to circ(), since any arc that hits all four quadrants will necessarily have a full semicircle in it, meaning you can draw two of the quadrants with one clip()/circ() pair.
(It's actually a little more complicated than that, but the upshot is that you never need more than 3.)
Anyway, cool to see other people working on the same puzzle. :)

I just spent an hour on this after realizing it's always possible to draw an arc with two calls to circ(), since any arc can be split into two halves, and any half arc can be drawn with one clipping rectangle.
I came up with something that works for about 75% of cases and got frustrated dealing with flipping angles, one pixel gaps, etc.
I'll probably try to tackle this again later, if no one else reads this and implements the two-circ solution before I need it for a game.

There's a mistake in your assumptions. It's not true that any half-arc can be drawn (properly) with only one clip rectangle.
Consider an arc that begins in octant 0 (0..45°) and ends in octant 3 (135..180°), but at a different rasterized y value. This is no more than half a turn. Both ends of the arc require a y>=ymin horizontal clipping plane, but at different y values. A clip rectangle obviously only has one y>=ymin plane. You can't use an x>=xmin or x<=xmax vertical plane because a rasterized circle's pixels can stack up vertically in those octants, making it impossible to clip at every pixel-precise y value with a vertical clipping plane.
Long story short, you need two clip rectangles for some half-arcs.
Luckily, you can always split a longer arc so that it never needs more that three.

Good catch, I missed considering that case. I wonder if it would be faster to draw a third circ or to just pset the very few offending pixels in the cases you describe.

Hard to say.
Usually zep is very generous with gpu cycle counts, coming in at 1 pixel per cycle (plus api call overhead), up to (I think) 8 pixels per cycle in a solid-filled shape.
An edge-to-edge circ() only taps around 362 pixels.
One octant of an edge-to=edge circ() can have same-row or same-col spans from 1px to about 7px, looks like. Probably about 3px on average.
So if you could calculate the (correct per PICO-8 circ() gpu behavior) pixels to fill in <= 120cyc/px each, then you'd break even or do better. Is it worth the tokens? Dunno.
Also of note is that a circ() almost certainly never draws a multi-pixel span right next to the diagonals between octants. For instance, the radius 63 circle on my screen doesn't start stacking pixels until it's 3 pixels away from the diagonal. I'm sure you can compute the size of this gray area between diagonally-neighboring octants and thus pretend an arc that begins near the end of, say, octant 0, is as ripe for x<=xmax clipping as an arc that starts in octant 1. It depends though on how the circle is generated by the GPU. With subpixel accuracy at the diagonal, this idea is bunk, as you could get a stack in the very next row/col.
Edit: never mind the paragraph above, the gpu definitely does stack right at the diagonal sometimes:




Here we go, three clips, three circs, some minor off-by-one caused by clipping rounding shenanigans that I am pursuing elsewhere.
The code can probably be significantly token golfed, but here it is from this cart:
function roundtozero(x) return x<0 and ceil(x) or flr(x) end function roundtoinf(x) return x<0 and flr(x) or ceil(x) end -- attempt to split an arc in thirds and draw each third with one clip() and one circ() function arc(x, y, r, a1, a2, ...) if (a1 == a2) pset(x + r * cos(a1), y - r * sin(a1), ...) return a2 = a2 + (a1 > a2 and 1 or 0) -- ensure a2>a1 local a3 = a1 + ( a2 - a1) / 3 for _=1,3 do local dx1, dy1, dx2, dy2, rev = r * cos(a1), r * -sin(a1), r * cos(a3), r * -sin(a3) local sx1, sy1, sx2, sy2 = dx1, dy1, dx2, dy2 if (min(abs(dx1),abs(dx2)) < min(abs(dy1),abs(dy2))) then -- arc endpoint closest to an axis is closer to x=0, swap coordinates dx1, dy1, dx2, dy2, rev = dy1, dx1, dy2, dx2, true end -- arc endpoint closest to an axis is [now] closer to y=0 for _=0,1 do -- first loop handles y coords, second x, with two swaps along the way if (abs(dy1) > abs(dy2)) dy1, dy2 = dy2, dy1 -- dy1 is [now] closer to y=0 than dy2 is -- clip rounding bugs cause problems here dy2 = roundtoinf((r+1) * sgn(dy2-dy1)) dy1 = roundtozero(dy1) if (dy1 > dy2) dy1, dy2 = dy2, dy1 -- dy1,dy2 now describe one axis of the clip box dx1, dy1, dx2, dy2 = dy1, dx1, dy2, dx2 -- swap coordinates end if (rev) dx1, dy1, dx2, dy2 = dy1, dx1, dy2, dx2 -- reverse earlier swap clip(x+dx1, y+dy1, dx2-dx1, dy2-dy1) circ(x, y, r, ...) clip() pset(x+sx1, y+sy1, 12) pset(x+sx2, y+sy2, 8) a1, a3 = a3, a3 + (a3 - a1) -- advance to the next third end clip() end |

It occurs to me that all this really is is a binary space partitioning problem. Find the minimum number of axis-aligned BSP planes and fit cliprects to them.

Not sure if the image uploaded correctly, but a thought:
For ... I want to say any arc smaller than a half-rotation? If you pick out either the arc itself or the missing part of the arc, whichever is smaller, and draw a horizontal line and a vertical line to define a box around that?
I think that splits the circle into the drawn arc plus missing arc, with the entirety of each on each side.
For the smaller arc, use that one bounding box to draw it in one clip(); for the larger arc, use "the other side of the horizontal line" + "the other side of the vertical line" to draw it in two.
Edit: fixed broken image - the forums don't like spaces in file names, I think.

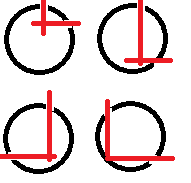
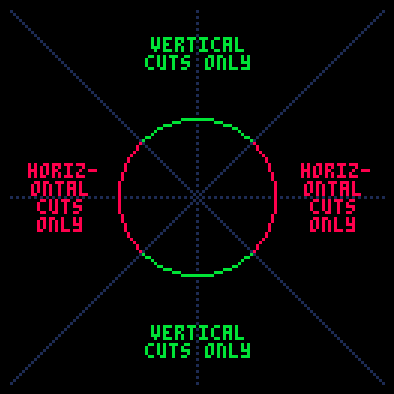
You're kinda dancing semi-safely around the diagonals in your example images. Keep in mind you can't use a horizontal cut safely in the 2nd,3rd,6th,7th octants, nor a vertical cut in the 1st,4th,5th,8th octants.

Oh, and a warning for anyone toying with this:
Beware of a little gotcha, where you think you can do 180° of an arc from diagonal to opposite diagonal with a single clipping rectangle. Some of the time you can, but some of the time this happens:

Basically, the circle in my previous example would be safe, because it didn't draw a pixel right on the diagonal, but this one does.
[Please log in to post a comment]