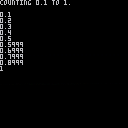
I was interested in making a type of high-number integer counter relying on the length and accuracy of 4-digit decimal numbers less than 1 when I came across this little slice of misfortune.
Here is the source to see there is no complication on my part:
-- real numbers are flawed!
function key()
repeat
flip()
until btnp(4)
end
b=1
e=10
for i=1,5 do
cls()
?"counting "..b.." to "..e.."."
key()
?""
for i=b,e,b do
?i
end
key()
b/=10
e/=10
end
?""
color(10)
?"complete!"
repeat
key()
until forever
|
Any solutions on how to get the correct numbers here ? And ... does this error extend to LUA or just Pico-8 ?

It extends to all computer representations of floating-point numbers. That cart demonstrates a Floating-Point error. It's not PICO-8's fault. It's not Lua's fault. It's a very common bug in programming, and it's not really preventable afaik.
Here's a section of the Wikipedia article for Floating-point arithmetic.
And here's the same error demonstrated in my browser:
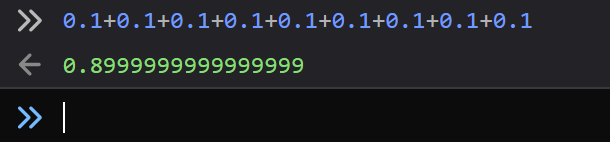

It makes no sense though, @TheV360.
I mean AFAIK decimal numbers just added or subtracted should not be retrieving a wrong value. I wrote code earlier to show you could add and subtract any number of digits, well past trillions:
https://www.lexaloffle.com/bbs/?tid=35715
Granted I had planned to use multiply and divide for these real numbers in my current experiment, but surely it can ... merely add and subtract by .1, .01, .001, and .0001 ?
And I know this error did not occur on the TRS-80 or Apple ][ computer. Because I used floating point numbers then.
Is this some type of encroaching error that has been carried through future OS and never resolved ?
Alright, let's focus for a second then.
Is there a perfect solution or common kludge used today to get past this ?
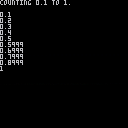
Now I was trying THIS, and it works, but I don't know how FAR it works, nor is it a good solution as it expects a truncation based on the value itself, which could mess up during complex calculations:

-- real numbers are flawed!
function key()
repeat
flip()
until btnp(4)
end
b=1
e=10
for i=1,5 do
cls()
?"counting 0 to "..e.."."
key()
?""
for j=0,e,b do
n=j
n=n+(b/2)
n=sub(n,1,i+1)
?n
end
key()
b/=10
e/=10
end
?""
color(10)
?"complete!"
repeat
key()
until forever
|

Floating point math is.... iffy. See this great video for a good explanation:

SOLUTION !
Yessiree ! I definitely found a way to fix it.
First off, try this, cause this is weird.
a=0 a=a+.5/10000 ?a |
You get zero as you would expect cause it's smaller than .0001 which is the limitation on variables.
But now try this in immediate mode with the code above:
b=0 if a!=b then print"error" end |
THEY DO NOT MATCH !
So surely one of them is a string, right ? I mean you only have a few variable types, string, table, or number. There is nothing further, right ?
Let's check:
?type(a) ?type(b) |
No, they're both numbers. But ... somehow different. Despite both containing only zero. So ... what's going on here ?
Wow, I wish I knew. :D
But, we can use this to repair our numbers, and we don't need an index to keep track of now. Here is the first code above with solution:

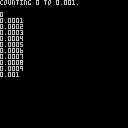
Here is the final code:
-- real numbers are repaired!
-- by dw817
function key()
repeat
flip()
until btnp(4)
end
b=1
e=10
for i=1,5 do
cls()
?"counting 0 to "..e.."."
key()
?""
for j=0,e,b do
n=j+.5/10000
?n
end
key()
b/=10
e/=10
end
?""
color(10)
?"complete!"
repeat
key()
until forever
|
So ... is that all it is ? That single line where you add .5/10000 and ... despite that calculated value by itself clearly being zero it somehow fixes it ? Yep. And that's fine, I'll use that method if that's what it takes to get "accurate" values.
Truth is often stranger than fiction. I think that is happening here.
Now, would someone like to explain WHY this works ? :)

Eye (O)(-) opening ! I recommend anyone having problems with floating point to watch the video.
The most important thing stated is (1/3) x3, which we understand as humans being the value of 1 is NOT the same as 0.333333333 x3 to a computer which is 0.999999999.
SO ! Therein lies the problem. And, no, I can't see an easy solution around it.
Perhaps future fantasy consoles or even computers for that matter might have something called the "human" factor, optional in math, which looks at a calculation and tries its level best to calculate the way a human would - and more importantly, to return a HUMAN value that makes sense. In this case,
a=1/3 b=a*3 ?b |
Would in fact return the value of 1.
. . .
Still doesn't explain why there can be two variables both with zero and yet ... according to a comparison, they somehow do not match.

To put it simply, print is lying to you. Numbers in pico-8 are 16:16 fixed point numbers(according to the manual). So technically they are not floating point numbers, though the video is still helpful as for how values less than 1 or represented. The 16:16 means that each side of the decimal point is represented by 16 bits or 2 bytes. To see the hexadecimal value of a number use:
tostr(num,true) |
For .0001 this returns 0x0000.0006. This tells us that we can go a bit smaller. However, using
tostr(0x.0001) |
will return 0. This value still exists though.
tostr(0x.0001,true) |
will return 0x0000.0001. And, if we follow your example
tostr(.5/10000,true) |
will return 0x0000.0003.
Here is your demonstration with hexadecimal values added.

Zero zero zero three !
The cake is a lie ! But I LOVE cake. Well, actually like. Pie if it's done right is much better.
Still, PRINT being deceptive ? I would not have expected this. Question. Is it possible to squeeze out a 5th decimal place now since apparently it does indeed exist and PRINT is merely not displaying it ?
Hmm ... this changes so much and explains why zero did not equal zero earlier.
Thanks, @Shoxidizer !

You won't be able to get a whole extra tenths place, there are not enough values smaller than .0001.
The attached program displays how a given value is display, it displayed as a fractional form, the value that its displayed value generates, and how that is displayed.
By the way, you ever try these in the console?
print(.0001) print(.0002) print(.0003) |
One of these is not like the others.

Definitely, @Shoxidizer. .0001 is coming out zero. Makes me wonder how all those great 3D programs execute as well as they do without running into errors.
And your Hexadecimal program above ? Newest gadget to explore. Saved to my folder of favorite offline games. Very interesting to play with. :D
Decimal of string of decimal is especially an area I want to experiment with.
[Please log in to post a comment]