Hi,
I am trying to come up with a simple algorithm for filling an area of the screen a particular color.
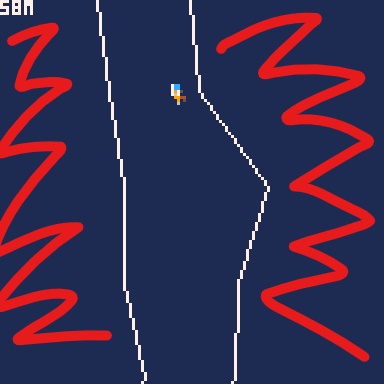
I have a "path" in my game defined by the thin white lines shown above. Lines are represented with the following data structures:
function mkvec(x,y)
local v=
{
x=x,
y=y,
getlength=function(self)
return sqrt(self.x^2+self.y^2)
end,
getnorm=function(self)
local l = self:getlength()
return mkvec(self.x / l, self.y / l);
end,
}
return v
end
----------------------------
function mkline(x1,y1,x2,y2)
local l=
{
a=mkvec(x1,y1),
b=mkvec(x2,y2),
draw=function(l,col)
line(l.a.x,l.a.y,l.b.x,l.b.y,col)
end,
drawnear=function(l,o,col)
local lp=closestpointalongline(
l.a,l.b,mkvec(o.x,o.y))
circ(lp.x,lp.y,2,col)
end,
closest=function(l,o)
return closestpointalongline(
l.a,l.b,mkvec(o.x,o.y))
end,
}
return l
end
|
I would like for the areas on the left and right of the path (the part with red thick lines scribbled in) to be filled a different color.
My current plan is to define a directional vector for corner to corner, and walk the line one pixel at a time, draw a line from there to the edge of the screen.
These feels a little hackish, so I'm wondering if there is something better! I suspect this may be a polygon fill algorithm, but since this problem set is some limited, I thought there might be a simpler way.
I also suspect that my pixels wont like up with the edge of the line, leaving small single pixel gaps.
Thanks!

Given the start and end points for each segment (x1,y1) and (x2,y2), find the equation for the line: y = mx + b, or x = (y - b) / m. m is the slope of the line = (y2-y1)/(x2-x1). Solve for b using one of the points: b = y1 - x1 * (y2-y1)/(x2-x1)
For each y between y1 and y2, find x using x = (y - b) / m. Alternatively for each x find y using y = mx - b. To fill to the right, draw a line from (x, y) to (127, y). To fill to the left, draw a line from (0, y) to (x, y).

Here's a demo:
function fill_side(x1, y1, x2, y2, col, is_left)
local x, y
-- offset for rounding
if not is_left then
x1 += 1
x2 += 1
end
local m = (y2-y1)/(x2-x1)
local b = y1 - x1 * m
for y=min(y1,y2),max(y1,y2) do
x = (y-b)/m
if is_left then
line(0,y,x,y,col)
else
line(x,y,127,y,col)
end
end
end
function _init()
px = 30
py = 30
ex = 60
ey = 90
side = false
end
function _update()
if (btn(0)) px -= 1
if (btn(1)) px += 1
if (btn(2)) py -= 1
if (btn(3)) py += 1
if (btnp(4)) side = not side
end
function _draw()
cls()
fill_side(px, py, ex, ey, 8, side)
line(px, py, ex, ey, 7)
end
|
I offset the fill by +1 when filling to the right because rounding puts the fill over the line by one pixel. This doesn't happen when filling to the left.
This version doesn't correctly handle the edge cases where y2=y1 or x2=x1. This is left as an exercise. ;)
(edit: cleaned it up some)

Might be faster and fewer tokens to draw the background over the whole screen, then fill the path over it.

You'd have to figure out which left and right segments are involved for each y. You could sort them into left and right sets and march down them as you cross each boundary. Whether that's fewer tokens I don't know. It would be one less line() call.

Rectfill commands are faster than horizontal lines for this sort of rasterization. If you want to get really fast, memset screams, but you are stuck filling in 2 pixel wide blocks unless you add code for the end pixels which would surely slow things right down again.

If this is a vertical scroller after all, another idea to consider is storing each raster line in a 128-element array, push new rows to the bottom, and pop off the top with DEL(). (Or do a rolling index.) Then you can use the array for drawing and collision.
[Please log in to post a comment]