Log In  



expint(): Counting To Eleventy-Bajillion In PICO-8 With Exponential Integers

Cart #mcg_expint_test-1 | 2025-05-30 | Code ▽ | Embed ▽ | License: CC4-BY-NC-SA

Overview

Hello, everyone! I'm back with another Quick 'n' Dirty code snippet: extreme range, low precision Exponential Integers!

expint() lets you easily work with extremely large numbers at low precision in PICO-8. You can create them, add to them, "spend" from them, display them in a friendly format, and save/load them using a single 32-bit data slot.

expint() is particularly well-suited to games where you need to track very large amounts of points or money, like incremental games/idle clickers, large-scale exploration games, and other places where 32k just isn't gonna cut it.

The Snippet And Its Use

Install

Paste the following snippet into your cart:

 
function expint(new_sig, new_exp) 
	local num = {}

	function num._step_up(steps)
		while steps > 0 do
			num.sig \= 10
			num.exp += 1
			steps -= 1
			if num.sig == 0 then -- we've lost all precision; for whatever we're doing, this number is as good as zero
				num.exp += steps
				steps = 0
			end
		end
	end

	function num._norm()
		while num.sig >= 10000 do
			num._step_up(1)
		end
		while num.sig < 1000 and num.exp > 0 do
			num.sig *= 10
			num.exp -= 1
		end
	end

	function num.add(val, sig)
		local to_add = expint(val, sig) -- be non-destructive with arithmetic; copy info into another expint to protect precision
		to_add._step_up(num.exp-to_add.exp) -- instead of doing any logic, just run step_up 
		num._step_up(to_add.exp-num.exp) -- on both the numbers. It'll only affect one of them.
		num.sig += to_add.sig
		num._norm()
	end

	function num.spend(val, sig)
		-- if val < num, subtracts val from num and returns true
		-- otherwise, returns false
		local to_spend = expint(val, sig)
		if to_spend.exp > num.exp or (to_spend.exp == num.exp and num.sig < to_spend.sig) then
			return false -- to_spend is greater than num; can't make the spend
		end
		to_spend._step_up(num.exp-to_spend.exp) -- instead of doing any logic, just run step_up 
		num._step_up(to_spend.exp-num.exp) -- on both the numbers. It'll only affect one of them.
		num.sig -= to_spend.sig
		num._norm()
		return true
	end

	function num.print()
--		local suffixes = split("K,m,g,T,P,E,Z,Y,R,Q") -- SI suffixes
		local suffixes = split("K,m,b,t,qU,qI,sX,sP,oC,nO,dE") -- number suffixes
		local return_string = num.sig
		if num.exp > 0 then
			local modval = num.exp%3
			local suffix = ((num.exp-1)\3+1)
			if suffix > #suffixes then
				return_string = sub(return_string,1,1).."."..sub(return_string, 2).."X10^"..(num.exp+3)
			else
				if modval != 0 then
					return_string = sub(return_string, 1, modval+1).."."..sub(return_string, modval+2)
				end
				return_string = return_string..suffixes[suffix]
			end
		end
		return return_string
	end

	function num.save(cart_slot)
		dset(cart_slot, num.sig | num.exp>>16)
	end

	function num.load(cart_slot)
		num.sig = dget(cart_slot)\1
		num.exp = dget(cart_slot)<<16
	end

	num.sig = new_sig
	num.exp = new_exp or 0

	-- handle special cases: input can also be either an integer in string format or a table (assume it's another expint()!)
	if type(new_sig) == "string" then
		num.sig = tonum(sub(new_sig, 1, 4))
		num.exp = max(#new_sig-4, 0)
	elseif type(new_sig) == "table" then
		num.sig = new_sig.sig
		num.exp = new_sig.exp
	end

	num._norm()
	return num
end

At present, this snippet uses 364 tokens; Shrinko-8 will reduce this to 358.

Instantiate

To create a new expint(), you can do one of the following:

 
w = expint(1,4)     -- significand, exponent: in this case, 1x10^3, or 10000
                    -- values must be whole numbers between 0 and 32767 (inclusive)

x = expint(10000)   -- built-in number type
                    -- whole numbers only between 0 and 32767 (inclusive)

y = expint("10000") -- a whole number as a string; digits only
                    -- can be as long as 32,767 characters, which is frankly silly

z = expint(y)       -- create a copy of an existing expint

Manipulate

 
x.add(y)     -- add the value of y to x
x.spend(y)   -- if y < x, subtract the value of y from x and return true 
             -- If y > x, make no changes to x and return false

-- NOTE: add() and spend() will accept all the same parameters as expint() above

Display

 
x.print()   -- returns the current value of x using a compact, human-friendly format

x = expint(10001)
print(x.print())
> 10.00k

Store

 
x.save(1)   -- saves the current value of x to the cart data slot provided
x.load(1)   -- loads the cart data from the slot provided into the current value of x

-- NOTE: you must call cartdata() before using save() and load()

Discussion

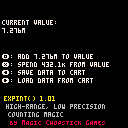
The Problem

One of the great things about PICO-8 is that invites you to look for ways to work around its stringent limitations. One of the biggest limitations I've found myself repeatedly bumping up against is, quite simply, "I want to count higher than 32 thousand, dangit!"

I've used a variety of solutions in the past, all adequate for their various purposes, but none of them really satisfying–and none of them good for really ridiculously high counting. All told, I set out to find a counting system that met the following criteria:

  • I want to be able to count big numbers. Just bonkers, bonkers big numbers, stupid huge numbers, thankyouverymuch
  • I don't want to spend too many tokens getting there
  • I want to support earning (add) and spending (subtract if less than) these numbers
  • I want to be able to easily create these numbers from an integer-as-string or built-in number type
  • I want to be able to display these huge numbers in a compact yet readable format
  • I don't need a lot of precision; if I already have a million points, a single additional point is meaningless to me.
  • I want to be able to save this huge number to a single slot of cart data (32 bits).

The Solution: Exponental Notation

Enter exponential notation. By using a significand (or mantissa) and an exponent, we can represent bonkers-high numbers in comparatively little space. Since space is always at a premium in PICO-8, we want to keep each of these numbers fairly small; in order to pack this into a single 32-bit space, we only want to use 16 bits each for the significand and exponent. (We could allocate this differently, but there are good reasons for doing it this way; see the Various Ramblings below for more details.)

With the expint() data type, we can store an almost arbitrarily large number to four significant digits. We can then represent that number in an exponential format, either in traditional scientific notation (1.234x10^4) or as a human-friendly string (12.34k). This suits PICO-8 quite well: you don't have much space to display your large numbers, and once you start getting into serious number territory, you can't even fit them on the screen anymore.

The Drawback: Also Exponential Notation

This is where the low precision comes in. Using expint(), 10,000 + 9 = 10,000. If you're doing important things, like flying an airplane or building a bridge, that's a very bad result! Happily, we're not doing important things; we're making video games! What's more, once you have ten thousand of something, another nine of that thing isn't going to be that big of a deal, especially if you're displaying that number as an approximation–for example, 10.13B instead of 10,132,449,018.

Other Limitations Of This Implementation

  • Whole numbers only. This isn't designed to work with negative numbers or non-integers, either in the significand or in the exponent. I haven't tried doing it, and I'm quite confident it'd behave badly if I did.
  • print() is a little weird right now. I want to further refine the print() function; right now, instead of showing 1.000k, it shows 1000, which feels...wrong. That said, it works for now, and it's still technically accurate. I think. :D
  • Even big numbers have their limits. We're still using a 16-bit number to hold our exponent; we can't go any higher than that. This will conk out around 999x10^32767.
  • This code is not particularly optimized for space. I'm confident that there are folks out there who will look at this, shake their heads at my foolishness, and proceed to strip this down to half its current size and twice its current speed. As an aside, Shrinko-8 will minify the verbose variable names quite nicely.
  • You can add, and you can spend, and that's it. Adding other operations should be fairly straightforward, but I'm limiting this release to the two biggies for most of the applications of this number type in PICO-8.
  • There are no guardrails. In an effort to save tokens, I'm not doing any real error handling or boundary testing here. There's nothing stopping you from driving this thing off a cliff.
  • I, uh, haven't really tested this all that thoroughly yet. The happy path works, but there are probably some real forehead-smackers floating around in here. Set me straight in the comments, please!

Various Ramblings

At first, I thought about doing a true single-precision floating point number implementation. This, after all, is industry standard, and there are plenty of implementations I could crib off of to make this happen. Before long, though, I stumbled across a common enemy: all of these implementations were way more token-intensive than I was looking to do. (This, I suspect, is why we don't see a bunch of floating-point custom types kicking around the forums for this purpose.)

So scratch going the IEEE route; given what I know about PICO-8, my most likely path to success would be to look for nifty, imperfect ways to leverage what the system already gives me.

Eventually, two separate but related concepts came together in my head like peanut butter and chocolate:

  • PICO-8 stores numbers as 16:16 fixed point decimals, neatly splitting them down the middle
  • @zep added some nice format flags to tonum() and tostr() to hack this 16:16 fixed point format into a 32-bit integer format

32 bits is nice, but still cuts you off a little over 2 billion, which for a lot of games isn't gonna cut it. What will cut it for this kind of game, though, is exponential notation: using a mantissa and an exponent, you can represent pretty much any number your heart can dream of. (Note that this is the basic concept behind standard floating-point implementations: so many bits reserved for the exponent, so many reserved for the mantissa.)

So I was kinda back where I started, but not quite: I realized I could use PICO-8's 16:16 fixed-point number format as a jumping-off point for a lot of shortcuts if I used it to store my mantissa and exponent in that same 16:16 layout. I could use some basic arithmetic and bitwise operators to cram the 16-bit significand and 16-bit exponent into the integer and fractional parts of the built-in number type for easy storage:

 
function num.save(cart_slot)
	dset(cart_slot, num.sig | num.exp>>16)
end

function num.load(cart_slot)
	num.sig = dget(cart_slot)\1
	num.exp = dget(cart_slot)<<16
end

1



[Please log in to post a comment]