This is a general purpose geometry/vector library.

It's based on Geometric Algebra (GA) but you don't need to know what that is to use it as most of the standard vector operations you're probably familiar with are here.

I'd be happy to add additional demos (with credit obviously) so if you make something interesting that you want to include let me know.

Updates

2024-04-21

• Added 3D triple pendulum demo (based on the 2D version here: https://matthias-research.github.io/pages/tenMinutePhysics/index.html)
  Hat tip to @shanecelis for this post (https://www.lexaloffle.com/bbs/?tid=54905) which made me aware of PBD and Matthias Müller.

 

gavel_demos

by jasondelaat

Cart #gavel_demos-5 | 2024-04-21 | Embed ▽ | License: CC4-BY-NC-SA

22

To get the library code itself, load #gavel_demos and then copy the algebra.lua file from /ram/cart/src to a convenient location.

Cheat sheet

I don't want to dive too deeply into the mathematics of GA here so this doesn't include everything but should include most of what people are probably already familiar with. Feel free to poke around the code and ask about anything that's not clear or that you just want to know more about.

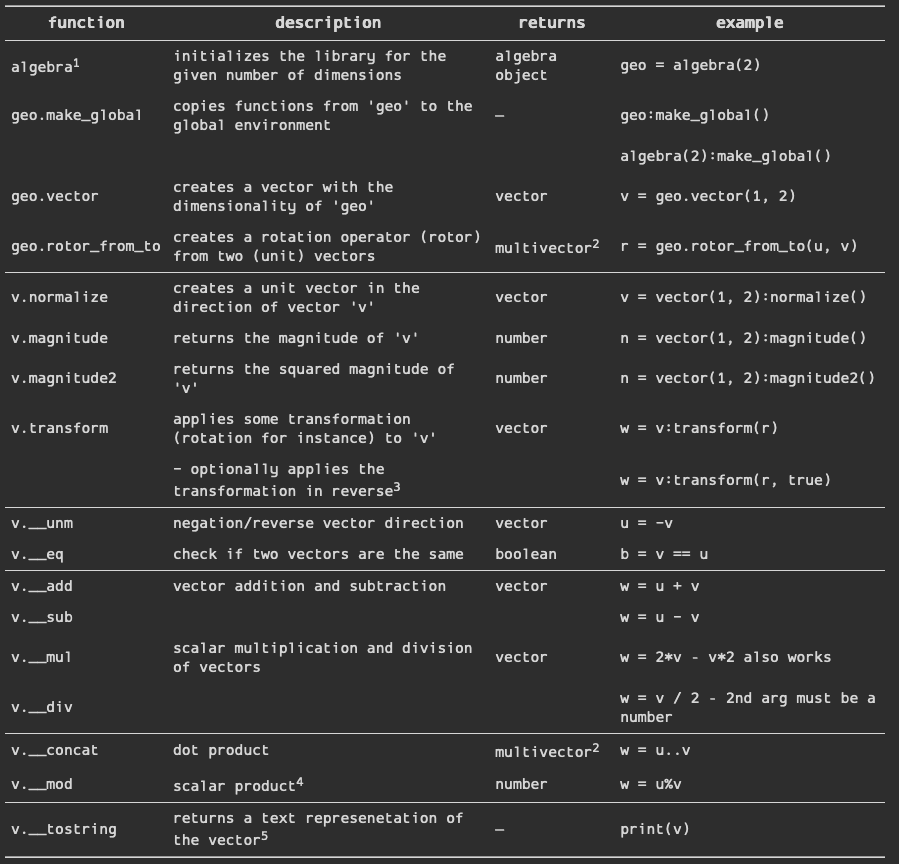
Notes

• 1 : GA is "component free" meaning you always work with the whole vector and not its individual components. That has a bunch of advantages but the most relevant one here is that you can pick how many dimensions you want---two, three, four, nine...eight hundred---and everything just works.
• 2 : Multivectors are a GA thing which you can think of as sort a more expansive vector. Technically vectors are also multivectors but with the "extra" components all set to 0. For simple usage you don't really need to know too much about them but it can be useful to know they exist.
• 3 : All tranformations are automatically reversible without having to build a whole new transformation. So if v.transform(t) rotates v clockwise then v.transform(t, true) will rotate it the same amount but counter-clockwise.
• 4 : For vectors---as opposed to general multivectors---the dot product and scalar product return the same value but as different types. For vectors u and v, (u..v).scalar == u%v
• 5 : string representations will look a bit weird. Since you can set any number of dimensions you want vector components are named by number. So print(vector(10, 20)) will display 10e1+20e2. You can think of e1 and e2 as x and y. As a small quality of life feature, you can access those components on a vector using either notation: v.e1 == v.x

There is one obvious thing missing that I should probably address.

Dude, where's my cross product?

GA's component free nature is what allows it to be general enough that you can just plug in a number of dimensions and have everything work. As you're probably aware, the cross product does not generalize to dimensions other than 3 so it's not here. What we have instead is the "wedge product" (__pow or ^ operator.) The wedge product does generalize.

In 3-dimensions the wedge product of two vectors and the cross product of two vectors contain the same information just presented slightly differently.

algebra(3):make_global()

u = vector(1, 2, 3)
v = vector(7, 5, 2)

print(u ^ v) --     -9e12-19e13-11e23

Don't worry, that's not a vector in 23 dimensions, it's what's called a bivector. Compare this result with the cross product of these two vectors:

u × v = (-11, 19, -9)

The order is reversed and the middle term is multiplied by -1. That seems like a tiny difference but it's the difference between a product which only exists in 3-dimensions and one that exists in any number of dimensions.(Although I'm being very hand-wavy here and there's more to it than that.)

You can write yourself a cross product function if you want to but learning to use the wedge product will usually make your code simpler and more general.

Will this actually work with 800 dimensions?

No. But that's just because it would be computationally infeasible not because there's anything wrong with the math. In principle everything would work in 800 dimensions. In practice you'd probably melt your processor. The way I've written it, GAVEL should work for anything up to 9 dimensions. It'll eat up a lot of memory and probably be slow but it should work. It could be expanded beyond 9 dimensions without too much trouble but I'm going to assume that if you're doing something requiring more than 9 dimensions you're (a) probably not doing it in Picotron, and (b) don't need my help.

Resources

Hopefully I'll make a proper geometric algebra tutorial at some point but until then here are some resources if you want to dive deeper into the math.

Geometric Algebra Playlist
<https://www.youtube.com/playlist?list=PLpzmRsG7u_gqaTo_vEseQ7U8KFvtiJY4K>;

Siggraph2019 Projective Geometric Algebra
<https://www.youtube.com/watch?v=tX4H_ctggYo&list=WL&index=3&t=634s&pp=gAQBiAQB>;

very interesting…will dig further. thanks for the pointers!

Thanks @freds72!
I only found out about GA around 2 years ago and it kinda blew my mind. I hope you find it as interesting as I have.

D? Is that a one piece reference?

@my_name_is_doof, certainly not an intentional one. I know literally nothing about one piece other than the name. Not a knock against it or anything, just outside of my interests