I know a lot of people have posted functions for drawing cubic bezier curves, but I'm tossing my own into the pot because why not. Just skimming threads, it feels like most people use pset() to draw them pixel by pixel; this one uses line() to draw them segment by segment.
Some animated gifs, because they're fun:
To save you digging into the cart, here's the two versions of the algorithm I'd recommend, based on my testing. If you want to see how fast they run, there's a pause menu item in the code that draws sets of 5000 random bezier curves with a bunch of different algorithm parameters in two sizes - 16-pixel square bounding box and 128-pixel square bounding box - and adds up the total CPU needed at 60 FPS.
-
The polynomial coefficients function. All of the other code uses this.
--coefficient fn (39 tokens, shared by all) function cubic_coef(p0,p1,p2,p3) --coefs for cubic bezier return p0, -3*p0+3*p1, 3*p0-6*p1+3*p2, -p0+3*p1-3*p2+p3 end
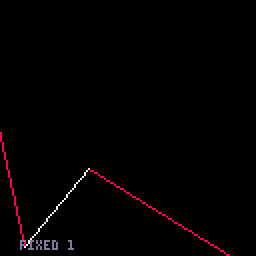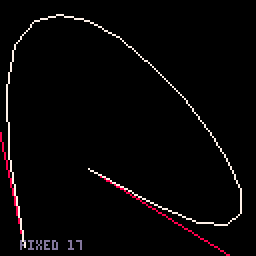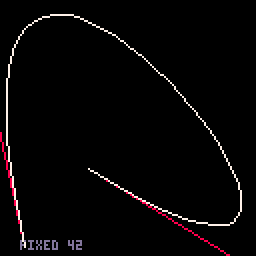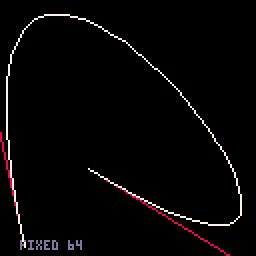
- Fixed-segments option. This one has 16 segments, which (a) is convenient numerically and (b) doesn't get too messy for small curves but doesn't look too chunky for large ones. From the benchmark, you could draw 220 big curves or 250 small curves in one 60 FPS frame.
--fixed 16 points (+80 tokens) function cbez_16(x0,y0,x1,y1,x2,y2,x3,y3) --cubic bez, dt predefined
--precalculate polynomial coefs
local a0,a1,a2,a3=cubic_coef(x0,x1,x2,x3)
local b0,b1,b2,b3=cubic_coef(y0,y1,y2,y3)
--set endpoint for first segment
-- by poking ram with coords
poke2(0x5f3c,x0) poke2(0x5f3e,y0)
-- --optional: clear error to avoid bugs
-- poke(0x5f35,0)--4 tokens
for t=0x.1,1,0x.1 do
line(
a0+t(a1+t(a2+ta3)),
b0+t(b1+t(b2+tb3))
)
end
end
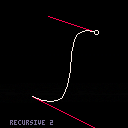
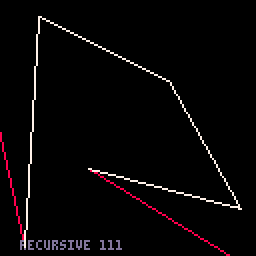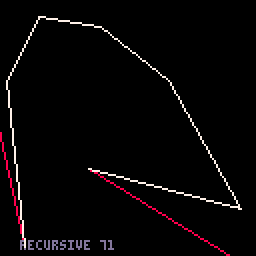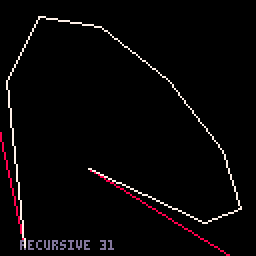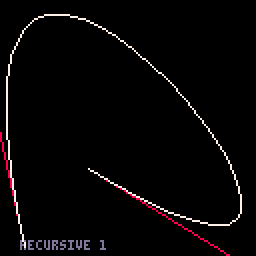
3. Adaptive-segments option. This one is a bit faster for small curves - like 320/frame - but much slower for large curves - like 110/frame. |
--recursive, fixed 2px precision
-- (+186 tokens)
function cbez_recurs2(x0,y0,x1,y1,x2,y2,x3,y3)
--cubic bez, adaptive points
--precalculate polynomial coefs
local a0,a1,a2,a3=cubic_coef(x0,x1,x2,x3)
local b0,b1,b2,b3=cubic_coef(y0,y1,y2,y3)
--set endpoint for first segment
-- by poking ram with coords
poke2(0x5f3c,x0) poke2(0x5f3e,y0)
-- --optional: clear error to avoid bugs
-- poke(0x5f35,0)--4 tokens
--poly function
local function xy(t)
return
a0+t(a1+t(a2+ta3)),
b0+t(b1+t(b2+tb3))
end
--subdividing draw function
local function crawl(tp,tn,xp,xn,yp,yn)
--draw curve recursively to tn
local tm=(tp+tn)>>1
local xm,ym=xy(tm)
--luchak fast abs
local xerr,yerr=(xp+xn)>>1,(yp+yn)>>1
xerr-=xm
yerr-=ym
if xerr^^(xerr>>31)>2
or yerr^^(yerr>>31)>2
then
--not precise enough; recurse
crawl(tp,tm,xp,xm,yp,ym)
crawl(tm,tn,xm,xn,ym,yn)
else
--close enough; draw
line(xm,ym)
line(xn,yn)
end
end
local x5,y5=xy(.5)
crawl(0,.5,x0,x5,y0,y5)
crawl(.5,1,x5,x3,y5,y3)
end
(Shoutout to @luchak, from whom I swiped this fast abs function - I think it ended up reducing runtime by about 3%, which might not be worth it but hey.) There's probably ways to optimize these further that I haven't thought of - I'm just not very good at that - so please feel free to sound off with any suggestions. Also, I tried to make good comments, but let me know if anything's unclear. |

Oh, I should mention the proximal inspiration for this: The Continuity of Splines, an hour-and-change-long documentary by Freya Holmér about different kinds of cubic splines and the challenges of making smooth curves. Great visualizations, great animations, great subtitles and narration - if popular mathematics is your jam, I fully recommend it.
[Please log in to post a comment]