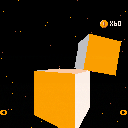
PIco3e is a 3D collision engine written in PICO-8! As far with the alpha release, what it does is...


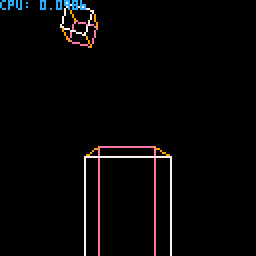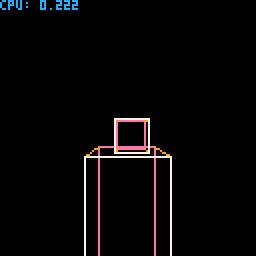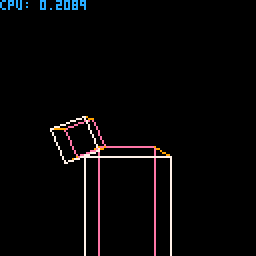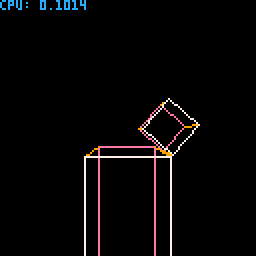
This was the alpha version, in wireframe. It does work with arbitrary rotated bodies and solve the forces correctly. It took me about 3 weeks of learning & coding, and below is the demo cart I've been using it for proof of work.
Implemented features from reference project qu3e:
- 3D Oriented Bounding Box (OBB) collision detection and resolution
- Discrete collision detection
- Collision test via the Separating Axis Theorem
- Collision manifold generation via face-to-face method and the sutherland clipping
Token usage: 2873 (with current scene). Thus space is sufficient for some game logic. Unfortunately cpu usage is a bit high, with collision between each 2 bodies takes 5% cpu in 30 fps and doubled in 60 fps. Therefore it's assumed optimal number of bodies is <= 4.
v1.0.0 Known issues:
- edge to face collision's force center is biased
- body doesn't rotate if supporting force is aligned to mass center
- cannot handle multiple body collisions / compound forces
And especially thanks so much to @freds72 without his help I couldn't make this happen.
Aug 13th, 2019. Update with a playable scene and fixed the edge to face collision bug.
Press Z to take a screenshot when the same color faces are aligned to camera.

For some reason I want to see more of known issue #2 😍
It's giving me some oddly satisfying feels.

@a2 As of speaking the bug should be gone. If anything similar happened again, please let me know!

[Please log in to post a comment]