To load this program in Pico-8, type:
load #sa |
Shuffling a deck of cards on a computer has come a long way, hasn't it ?
The classic method is to go through each card one at a time and shuffle them by taking the index card and swapping it with a random card anywhere in the deck.
The problem with this method is that after a shuffle if the first card is say 2 of Spades, then you already know the next card will be Ace of Spades. So, yeah, it's not perfect.
Another way is to create a table picking a random number from 0-51 adding it to an array until the deck is filled. This will work but it can be slow once it gets near the end picking that random number from 0-51 to get that very last card that is not in the deck.
Thus future coding now has two interesting commands, ADD and DEL.
Add will do just that, add a value on to an existing array placing it right at the end. If it's the first item, obviously it goes in the first place. But each new successive item is placed on the end. So if you wrote code like this:
a={}
add(a,1)
add(a,2)
add(a,3)
|
Then a would be an array starting with index 1 and contain 1, 2, and 3.
Now here is where DEL comes in and it's quite powerful what it does. In older code if we wanted to remove an item from an array you would have to create a reverse FOR/NEXT loop to copy all the older items one step above the item you were removing. I did this back in S2 and it was not speedy.
However, you do not need to do this in Pico-8, for instance, let's take our original code and remove the middle item:
a={}
add(a,1)
add(a,2)
add(a,3)
del(a,a[2])
|
Now the results are 1, 3. So with this in mind it does indeed ADD and DELETE items from the array. Doing so we can now make a proper SHUFFLE routine, where every single item in the array can be plucked out randomly, added to a separate array with ADD and neatly sealed closed from the original array with the DEL command.
And it does not swap existing items but actually pulls out each and every single item randomly to be placed in a 2nd growing array.
That is exactly what I am doing in this code, note two functions of use. SHUFFLE() which can shuffle a numeric or string array of any size as well as a function just for this code called PLOTCARD() which draws a small playing card on the screen.
Combining these functions you get a very good card shuffling routine that needs only one pass to make a perfect and completely random shuffle of a deck of cards, using our friend commands, ADD and DEL.

If you have a table of 52 cards, you could do:
for i=#deck,1,-1 do rnd_card=ceil(rnd(i)) deck[i],deck[rnd_card]=deck[rnd_card],deck[i] end |
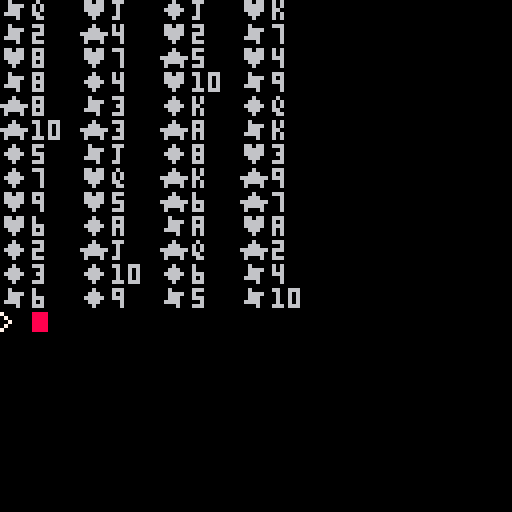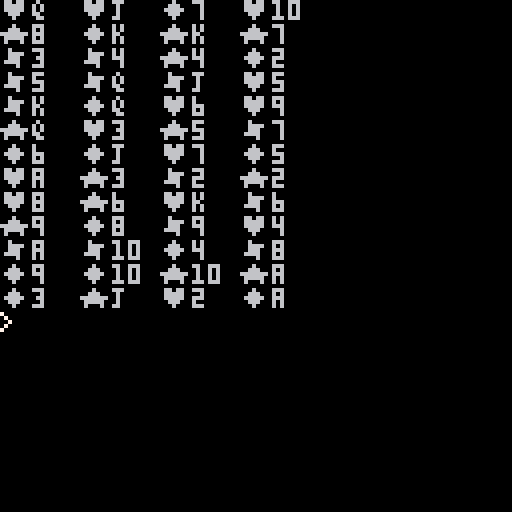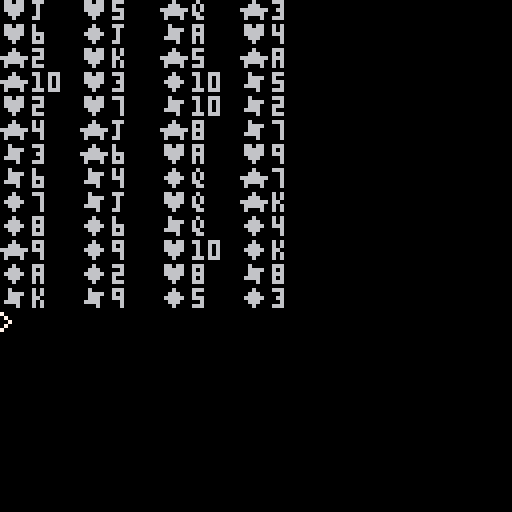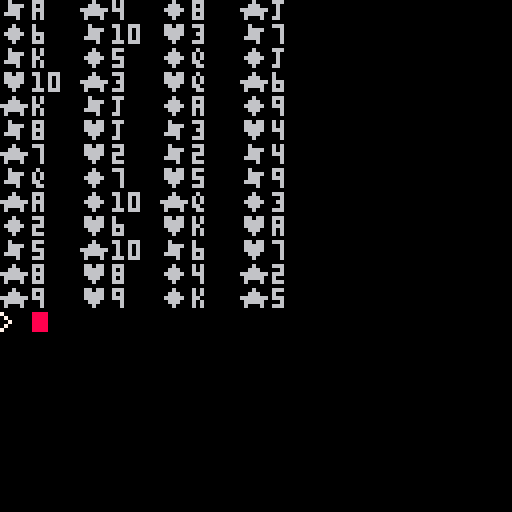

Ah, @MBoffin, but someone pointed out to me earlier that this is not a true randomization for the very method I mentioned in what I wrote above.
You are swapping two cards - and yes I agree, I would've done this except that it has problems.
For instance let's say you swapped the first card with the second, so the first card was Ace of Spades but is now 2 of Spades, then you would always know that the 2nd card is the opposite of the first, in this case, the Ace of Spades.
Using the ADD and DEL method you ensure a perfect randomization each time without swapping cards.
I've been using your method above for years which is also what I learned from David Ahl, but a different programmer said the SWAP method is not accurate for a good randomization and stated one perfect method using the sorted cards plucked out at random until they are all gone from the first array - which is the code I have above.
. . .
Your idea for a maze though still intrigues me where it snakes through and pulls back when stuck, very different from what I've learned.
I'm working on writing a book chapter right now but when I finish, I'll see if I can write a maze-making program just from watching your demo. If I get stuck I'll refer to the code but let me see if I can write it by concept alone - that will prove I understand it.

The method I posted is a very fast, unbiased shuffling method. It's a modern implementation of the Fisher-Yates Shuffle. Per the Wikipedia article on it:
"The algorithm effectively puts all the elements into a hat; it continually determines the next element by randomly drawing an element from the hat until no elements remain. The algorithm produces an unbiased permutation: every permutation is equally likely. The modern version of the algorithm is efficient: it takes time proportional to the number of items being shuffled and shuffles them in place." |
You're still picking random cards until you've picked all the cards. But instead of putting them in two arrays, where one gets depleted while the other is filled up, you just keep them all in the same array. You keep the chosen cards at the back of the array, and the unchosen cards at the front of the array. When you pick a random card from the unchosen section, you move it to the chosen section, so the unchosen section decreases by 1, and the chosen section increases by 1.

Finished my book chapter.
Yeah @MBoffin. I mentioned, I know this already.
And I'd like to use it but I also like the ability of true randomness in computer playing cards which apparently I did not think was possible at such a high speed - before what I wrote.
So - if I do make a game with cards, I think everyone's gonna like it lots cause it will be a really good and perfect shuffle and not the inaccurate swap method shuffle.
And it's not so bad. I understand the coding perfectly now for the insertion method. Here it is at a peak:
deck1={}
for i=1,52 do
deck1[i]=i
end
deck2={}
for i=1,52 do
r=flr(rnd(#deck1))+1
add(deck2,deck1[r])
del(deck1,deck1[r])
end
|
If you need output that's:
cls()
for i=0,3 do
for j=0,12 do
a=deck2[j+i*13+1]-1
b=a%13+1
c=flr(a/13)+1
print(sub("a23456789tjqk",b,b)..sub("schd",c,c),5+j*9,50+i*7)
end
end
?""
|
If it makes you feel any better I'll still resort to your variable swapping for good old bubble sort when I need it instead of those more advanced ones as I really only like to code stuff I understand.

I apologize, @MBoffin. I see what you are doing here now. That is indeed advanced, a perfect randomization and using only one array without array swapping.
Thanks for sharing this. Let me - fight this code for a bit and I'll get back to this.

@MBoffin your code is great, but I think there's a bug if you're using 1-indexing
rnd(x) generates a number between 0<=n<x
ceil() takes care of almost all (1-2^-64?) cases except for when rnd returns 0
then ceil(0) is 0 and we're off by one for indexing into the deck (assuming 1-indexing)
here's my fix
for i=#deck,1,-1 do -- rnd_card=ceil(rnd(i)) rnd_card=flr(rnd(i))+1 deck[i],deck[rnd_card]=deck[rnd_card],deck[i] end |
[Please log in to post a comment]