

This is a tool for creating and editing splines within your game. I used this initally for a shmup i was working on where I wanted to create an intresting enemy flight pattern.
The black area represents a 128x128 screen.
Just click in the points you want then press CTRL+C to copy to clipboard This will copy all points to the clipboard as a string.
This string can be then used within your game.

This is what I use it for.
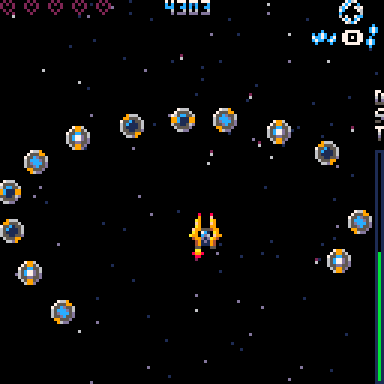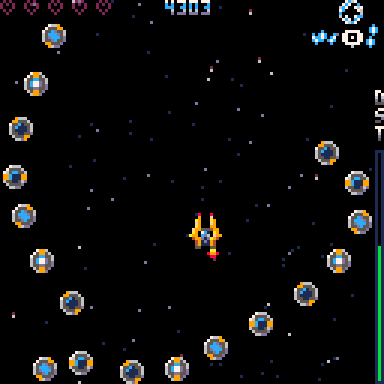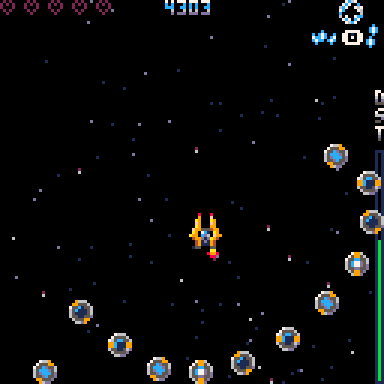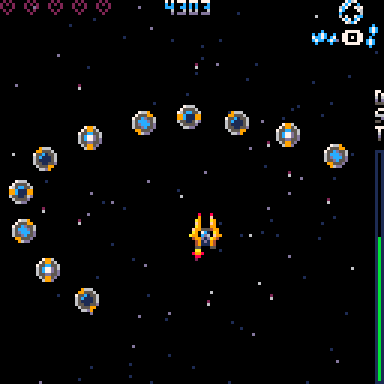
You can test out pasting of splines here. Also this cart has code for handling the splines.
How to use
Reading code
copy the following code to your cart (this can also be read from tab 2 of the demo cart)
--distance vunerable to overflow
function pdist(p1,p2)
return ((p2.x-p1.x)^2+(p2.y-p1.y)^2)^0.5
end
--cubic bezier single dimension
function cub_b_p(a,b,c,d,t)
local tm=1-t
return tm*tm*tm*a+
tm*tm*3*t*b+
tm*3*t*t*c+
t*t*t*d
end
--cubic bezier x&y
function cub_bez(p1,p2,p3,p4,t)
return {x=cub_b_p(p1.x,
p2.x,
p3.x,
p4.x,
t),
y=cub_b_p(p1.y,
p2.y,
p3.y,
p4.y,
t)}
end
--read splines
--expected table with multiple
--of 8 entries.
--p1.x,p1.y
function read_spline(points)
local curves,dists,td={},{},0
local limits={0}
for i=1,#points,8 do
local pts={}
for j=i,i+8,2 do
add(pts, {
x=points[j],
y=points[j+1]})
end
local function c(t)
return cub_bez(
pts[1],
pts[2],
pts[3],
pts[4],
t)
end
local d=0
for j=0x0.1,1,0x0.1 do
d+=pdist(c(j-0x0.1),c(j))
end
add(curves,c)
add(dists,d)
td+=d
end
local l=0
for d in all(dists) do
l+=d/td
add(limits,l)
end
limits[#limits]=1
local function spl(t)
if t==1 then
return curves[#curves](1)
end
local i,l=1,0
while t>=l do
i+=1
l=limits[i] or 1
end
local ol=limits[i-1]
local fact=1/(l-ol)
local t2=(t-ol)*fact
return curves[i-1](t2)
end
--return curves
return spl
end
|
2 Generating curves
Generate curves using the main cart that represent how you would like your mobs to move. Just click different points into place. Note that the black area represents a whole screen of 128x128 pixels.
You can click and drag points around, press delete to delete the last point. When you are happy with your curve press CTRL+C to copy a string to the clipboard.
NOTE: Sometimes the string doesn't copy correctly in the web player, if this happens from pico-8 you can load #spline and run the cart locally. The copy seems far more reliable when running in pico-8
Paste the following into your _init() function.
path=read_spline(split(*your pasted string*))
Then whenever you want a point along the path you just call path using the decimal of what portion of the path you want covered.
examples
local point = path(0) Will give you the start point of the path
local point = path(0.25) Will give you a point 1/4 the way through the path.
local point = path(1) Will give you a point at the end of the path.
local point = path(0.5) --half way spr(1, point.x, point.y) --draw sprite 1 at this point. |
Feel free to look at the demo cart for code that uses a sprite.
Update
Now cart accepts pasting of splines not just upload.
Now curves are more round by default
Credits
Thanks to @pancelor for the idea about the splines.
Thanks to @Heracleum for assistance writing up how to use the cart.

Man, I never thought about this, but pico 8 NEED a path editor. Kinda like the path editor from game maker. This does the work very well. Gold star.

@spellcaster there are multiple ways that this can be read. The approach I take is as follows.
--read splines
--expected table with multiple
--of 8 entries.
--p1.x,p1.y
function read_spline(points)
local curves,dists,td={},{},0
local limits={0}
for i=1,#points,8 do
local pts={}
for j=i,i+8,2 do
add(pts, {
x=points[j],
y=points[j+1]})
end
local function c(t)
return cub_bez(
pts[1],
pts[2],
pts[3],
pts[4],
t)
end
local d=0
for j=0x0.1,1,0x0.1 do
d+=pdist(c(j-0x0.1),c(j))
end
add(curves,c)
add(dists,d)
td+=d
end
local l=0
for d in all(dists) do
l+=d/td
add(limits,l)
end
limits[#limits]=1
local function spl(t)
local i,l=1,0
while t>=l do
i+=1
l=limits[i] or 1
end
local ol=limits[i-1]
local fact=1/(l-ol)
local t2=(t-ol)*fact
return curves[i-1](t2)
end
--return curves
return spl
end
--distance vunerable to overflow
function pdist(p1,p2)
return ((p2.x-p1.x)^2+(p2.y-p1.y)^2)^0.5
end
--cubic bezier single dimension
function cub_b_p(a,b,c,d,t)
local tm=1-t
return tm*tm*tm*a+
tm*tm*3*t*b+
tm*3*t*t*c+
t*t*t*d
end
--cubic bezier x&y
function cub_bez(p1,p2,p3,p4,t)
return {x=cub_b_p(p1.x,
p2.x,
p3.x,
p4.x,
t),
y=cub_b_p(p1.y,
p2.y,
p3.y,
p4.y,
t)}
end |
Take the array of points. Every number represents X,y pairs.
For every four pairs represents a segment. I run this through the function cub_bez() with a t between 0 and 1 which represents 0 is at the first point of the segment 1 is at the end point of the segment.
Depending on what you want to do this may be enough. However I'm using it for motion therefore I want to normalize all of this so that each segment is the same speed.
To do this I sample each curve segment multiple times and get a sum of the distance between each of the points.
I then add all of these together and produce a new function that takes a value between 0 and 1 that represents the entire spline as a single function.
This function is returned from the read_spline function below.
[Please log in to post a comment]








