Answer: Quite a few! But you probably have better options.
I've previously seen PICO-8 decoders for hex and base-64 strings. Recently I was curious: which base is most efficient? There are a lot more possibilities than just 16 or 64, and I knew PICO-8's code compression would affect the actual efficiency.
So I ran an experiment.
The experiment: I wrote a script to generate a bunch of .p8 files containing random data, and I exported them all through PICO-8 v0.2.2c to see how long the random data could get before PICO-8 would complain. The random data was in the form of strings in a given base: e.g., for base 16, the cart's entire program was x="(random hex string)". I generated these carts from base 2 (just "0" and "1") up to base 92 (almost every printable ASCII character). I ran several trials for each base because using random strings causes some variation in the measurements. I then counted the theoretical information content of each string (e.g., log-base-2 of the alphabet size) and converted the average for each base to kilobytes.
My initial hypothesis: There would be a few different sweet spots where the size of the alphabet would play better with PICO-8's code compression. Specifically, I had my metaphorical money on base 48 because the indexes 0-47 work well with PICO-8's move-to-front encoding.
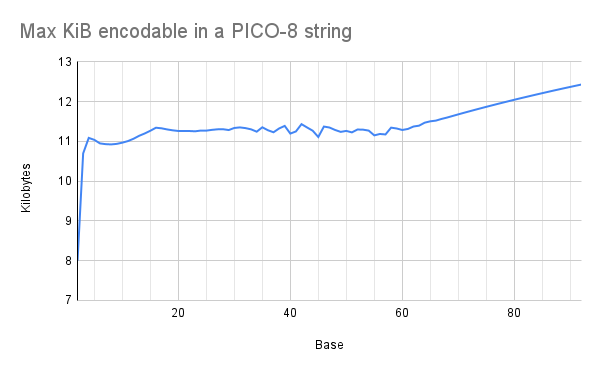
The actual result: There are no clear sweet spots! Small bases are less efficient, but efficiency plateaus around base 16. And if you go much higher than base 64, you get a gradual linear increase in efficiency.
So what's going on here?
It turns out that PICO-8 does a surprisingly good job of compressing strings. Even with a random hex string, you still get quite a few 4-digit substrings that occur multiple times in the data, just by chance (something something birthday paradox). PICO-8 can encode these repetitions efficiently (yay compression!), so even though a hex digit carries fewer bits of information than a base-64 digit, PICO-8 can store proportionally more of them.
(Note that this doesn't break any laws of data compression! PICO-8 is compressing random hex digits to around 5.38 bits/digit, whereas the theoretical minimum is 4 bits. PICO-8 isn't beating the universe. It's just beating its own move-to-front encoding, which can do hex digits at 6 bits/digit.)
The plateau happens because as the base increases, the data gets harder to compress. Each digits carries more bits, but the string cannot be as long because PICO-8 can't compress it as well, and the two factors cancel out each other.
The linear section after base 64 happens, I suspect, because when PICO-8 can't compress a section of the data, it falls back to encoding raw bytes for that section. So at that point, the base of the string doesn't matter -- it always costs 8 bits to encode each digit, no matter what the base is. I haven't tested it, but I suspect base-128 would work well if you had to stuff a whole lot of data into a string.
All that said, a lot of this isn't very pragmatic for actually making carts. There are better places to store binary data (e.g., the map section of the cart) and there are better ways to encode specific types of data (e.g., PX9 for images). But I had fun doing running this experiment, and I haven't seen any other discussions like this, so I figured I'd share the results in case anyone else was pondering similar things.

Here's a proof-of-concept for a base-128 decoder. All image data is stored in code. Press any button to switch images.
If you look closely, the bee image is very slightly letterboxed: I had to trim some pixels to get the data to fit within the 15616-byte compressed size limit. And just barely!
- Compressed data size: 15615
- If you replace
datawith empty string: 384
There's definitely some optimization that could be done here to get that 384 bytes down. I spent practically zero effort on optimization; maybe if I did, I could get the whole bee to fit.
Again, there are better ways to do this. Instead of storing the image data in a string and having the decoder copy it to the first 0x4000 bytes of memory, I could just... store the image data in the first 0x4000 bytes of the cart, and not have a decoder function at all. Pretty much the only reason you would ever want to do this is if you had more data than could fit in the cart's first 0x4300 bytes.

Great work! Why stop at 92, by the way? I think even larger bases are worth a try.
Oh and even though it’s outdated now, you may find this thread interesting, too!

Oh wow, you've done a ton of research on this! Thanks for the link; this stuff is super interesting. You mentioned it's outdated and I'm curious why -- is it because Zep has since added a fallback mode for incompressible data?
Larger bases are definitely worth a try, and I do want to play around with them more. As for the experiment I ran the other day, I think I already got a pretty clear picture of how larger bases behave. For base-68 and above, PICO-8 always gives up on compressing the data, and every cart ended up with exactly 15612 digits in the data string. So beyond that point, the graph ought to just be a plot of 15612*log2(x)/8/1024, more or less.
The result you got for base-2 is pretty wild. My experiment was trying to pack in as much data as possible, which caused base-2 to run into the uncompressed size limit. Now I really want to run an experiment with a variety of different data sizes.

Holy cow, PICO-8 has ord() now! Now I can get rid of those lookup tables.
I'm playing around with zep's method of directly storing the data in the string (base 256?). As one might guess, it's more efficient than base 128: the theoretical maximum for base-128 data in a cart is about 14.3 KiB, but with encoding random bytes in base 256, I can get at least 14.8 KiB, and that's with a less-than-optimized decoder taking up some of the space.
Fascinating stuff. Thanks @merwok!

I ran a couple more experiments and got a couple more graphs.
First experiment: I was curious about the results that @samhocevar reported, that raw binary was (at least theoretically) more efficient than some of the higher bases. So I generated a bunch of random byte strings of various sizes, encoded them using various bases (powers of 2), and measured the compressed sizes of the resulting carts.
Also, for the sake of realism, I included a decoder function with each data blob. Decoders may vary in size (e.g., a hexadecimal decoder is a little easier to make concise than a base-64 decoder), and I was curious if that would be visible in the numbers.
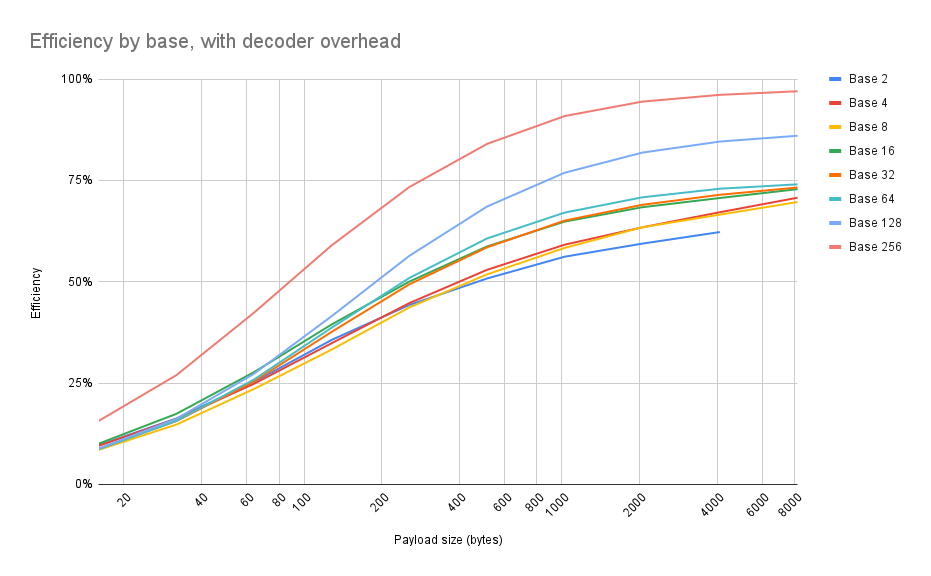
tl;dr: Base 256 (i.e., 1 string character == 1 byte, like how zep suggested here) is always the best. Always use base 256.
It's hard to see on the graph, but here's the actual numbers. There are, in fact, inversions such as base 16 sometimes being more efficient than base 64, or binary being better than some higher bases for short strings. But from a practical standpoint, it doesn't matter: for every size payload that I tested, base 256 always beat the other bases.
Payload Base 2 Base 4 Base 8 Base 16 Base 32 Base 64 Base 128 Base 256
16 9.68% 9.54% 8.54% 10.06% 8.84% 8.70% 8.87% 15.69%
32 16.27% 16.16% 14.77% 17.42% 15.64% 15.69% 16.19% 26.97%
64 25.30% 24.84% 23.56% 27.71% 25.43% 25.88% 27.31% 42.38%
128 35.65% 34.85% 33.28% 39.47% 37.65% 38.67% 41.51% 58.99%
256 44.27% 44.73% 43.66% 50.03% 49.36% 50.93% 56.39% 73.35%
512 50.79% 52.93% 51.80% 58.69% 58.47% 60.66% 68.54% 83.98%
1024 56.17% 59.13% 58.34% 64.82% 65.07% 67.04% 76.88% 90.86%
2048 59.40% 63.41% 63.43% 68.37% 68.97% 70.82% 81.84% 94.42%
4096 62.25% 67.14% 66.55% 70.65% 71.45% 72.94% 84.57% 96.09%
8192 70.72% 69.66% 72.83% 73.24% 74.02% 86.01% 96.97% |
Second experiment: At what point does it make sense to do a custom string encoding versus built-in functions, like x=split"123,45,67"? Again, I generated a bunch of random byte strings of varying lengths, using either base-256 or split to encode them in a cart. For base 256, I included a decoder with the data for the sake of realism, as I did previously: I wanted the numbers to reflect the overhead of needing to bundle custom code with the data.
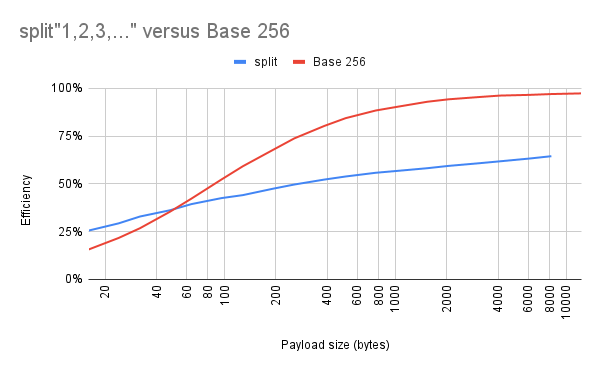
The break-even point is somewhere around 50 bytes. Above that point, it's more efficient in terms of compressed code size to store the bytes as characters in a binary string. But below that point, the size of the decoder dominates, and it's more efficient to use split.

Not necessarily all that surprising but it's nice to see such a thorough analysis and use cases where a simpler approach can be both easier and more—or at least similarly—efficient. And charts! Gotta love a good chart.
I had a fairly specific compression problem a while ago, Adventures in data compression, which you may (or may not) find interesting.

More experiments, more graphs!
Up to this point, the random byte strings I've been encoding have all been uniformly distributed: i.e., each of the 256 possible byte values had an equal chance of being chosen. But this is not what real-world data looks like!
I can't try every single possible statistical distribution, but Zipf's law is a common pattern to see in real-world data. For our purposes, suppose the most common byte value occurs k times. Then Zipf's law says that the 2nd most common byte will occur roughly k/2 times, the 3rd most common byte value will occur k/3 times, and so on.
Also, small numbers tend to be more common in real-world data. So for this next experiment, I made the zero byte (\0) the most common: it would make up about 16% of the random data. Value 1 (\x01) would occur half of that, or 8% of the time. Value 2 (\x02) would occur 5% of the time, and so on, according to Zipf's law. And after encoding all of those random byte strings (and bundling a decoder with the data, like before), the compressed code sizes look like this:
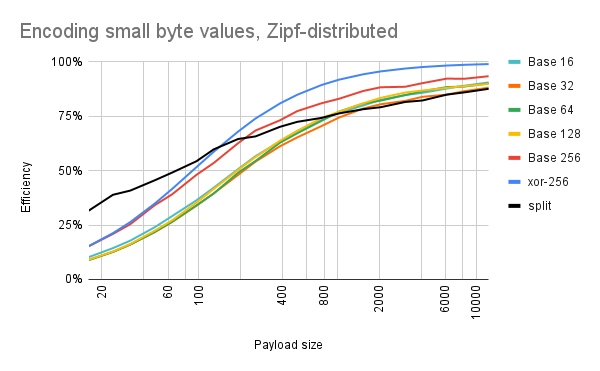
There's a new encoding scheme on the graph: xor-256. This is exactly the same as base 256, except that each byte value is XORed with a constant during encoding, and XORed with that same constant during decoding. I added this scheme because encoding small numbers is rough on base 256: this is because certain small numbers (0, 10, 13) correspond to escape sequences (\0, \n, \r), causing the base-256 strings to be slightly longer. You can see this in the difference between the two lines on the graph: xor-256 is always the most efficient, and base-256 falls to second place.
The code for xor-256 looks like this:
function decode(s) local i for i=1,#s do poke(0x7fff+i,ord(s,i)^^7) end end decode"ᵉb\r゜0ケ⁶.、¹、⁷J]⁷q>²⁘⁷□'⁴⁵リぬ¹ @⁷i⁷" |
In the above example, the XOR constant is 7 (see the ^^7 on line 4). This constant is chosen on a per-string basis: it is the smallest number that minimizes how many escape sequences are in the final string (at least roughly so).
(Also, I just realized that line 2, local i, is unnecessary. Whoops! This means the decoders for xor-256/base-256 could have been a fraction of a percent more efficient on my graphs -- not that it matters too much.)
Note also that using the built-in split function remains more efficient for longer: previously, for encoding uniformly-random bytes, the break-even point for switching to binary strings was around 50 bytes of data. Now it's closer to 150 if you do something similar to xor-256 (210 if you don't). I'm guessing two things are happening here: (1) 48% of the values are going to be single-digit numbers, which are easier to encode; and (2) because a minority of the values are making up a majority of the data, there are probably more coincidences where a run of values repeats -- allowing PICO-8's code compressor to swoop in and optimize things.
Okay, time for another experiment.
Not all data is composed of small numbers. For example, uncompressed image data could have bytes of any size, depending on the colors in the image. But the bytes aren't uniformly random, either: you will still have some pairs of pixels that occur much more often than others. Let's try to mimic this. What if, instead of always using \0 as our most popular byte, we pick some arbitrary byte to appear 16% of the time? And pick some other byte for 8%, and yet another byte for 5%, and so on?
Well, you might get a graph like this:
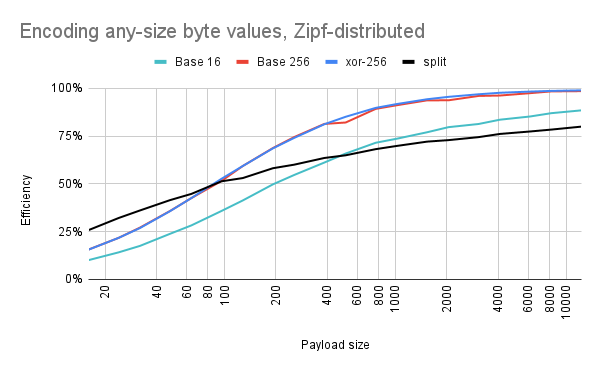
Base 256 is much more competitive again. There's still some random fluctuation: sometimes we get unlucky, and the popular bytes happen to correspond with escape sequences. In contrast, xor-256 is consistently "lucky" because it is able to assign the escape sequences to the least common byte values.
Also, split is slightly less competitive now: the break-even point is now around 90 bytes. Which makes sense, because more of the byte values will be larger now. The data still has a Zipfian distribution, though, so I'm guessing that PICO-8's code compressor is still seeing more runs of repeat data than it would if the encoded bytes were uniformly random.
So when should you transition from using split to using binary strings? The three break-even points we've seen so far are 50, 90, and 150 bytes (and maybe a fourth one at 210), so it really depends on your data. It also depends on whether you have more headroom in your token count or your compressed code size (split is more token-friendly), and how much you value the strings being human readable/writable (split wins this one, too).

@jasondelaat Thanks for the link! I enjoyed reading your post on SDFs. I especially liked the animated demo -- it really made it clear why you wanted to compress the underlying data, as opposed to bitmaps calculated from that data.
One thing that I think surprised both of us is that PICO-8 is actually pretty good at compressing data. When I started these experiments, I originally expected base 48 to be the winner -- when it turns out what you actually want to do is just shove raw binary data into a string and let PICO-8 handle it. And while it's not exactly the same, what you wrote about "Compressing less to compress more" feels like a very similar lesson.
Granted, there are still occasions where you, the programmer, are smarter than PICO-8, and you can do something to make the data more compressible: whether it's something simple like XORing data with a constant, or something more advanced like applying a vector transform to a SDF. But it's still a matter of how to best work with your tool, as opposed to trying to compress the data all by yourself.
[Please log in to post a comment]