accept_reject

by sugarvoid

Cart #accept_reject-1 | 2025-05-28 | Embed ▽ | License: CC4-BY-NC-SA

2

Update 1 5/28/2025 (thank you @Kistaro)

• Changed banker's offer to remove "low balling"
• Added number of cases to next round
• Improved setup code

I had a very lucky first run, but it showed that the algorithm for the banker's offers is lowballing too far. Offers far below the average result are interesting when you have a few high value boxes, a wide gap, and then a bunch of low value boxes, and the offer is inside that gap. But as I kept playing and getting very lucky with low draws, the offers barely went up; the increasing chance of uncovering a high-value box makes continuing to play increasingly risky, and the arbitrage in the real-world game show between "the banker plays many times, but you only get to play once" creates tension, but I don't think there was any way to justify the last two offers it made:

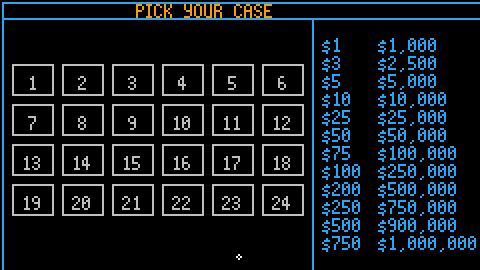
• Remaining: $25K, $750K, $1M; offer appx. $165K or something like that -- I don't remember exactly, I do remember it was notably below $250k which seemed absurd to me in the circumstances
• Final: $750K, $1M; offer is $437K, which is obviously pointless.

I accepted no offers and finished the game with my original case, containing $1M.

The game is obviously high variance, and the banker is supposed to lowball you! But "lower than the median" seems silly and "lower than the lowest remaining case" is extremely silly. Maybe trim that up a bit.

@Kistaro,
Thanks for the feedback.

I made this game in a vacuum, so I may have missed a few things that others would have noticed. The math for the offers was one of the early things implemented, it was quickly forgotten and never touched again. I will tweak it so its not so low bally. Thanks again for the feedback and for playing.

I've written a more interesting get_offer function for you:

function get_offer()
    local values_left = 0
    local sum, lowest = 0, 1000000
    for _, v in ipairs(game_values) do
        if v.in_play then
            values_left = values_left + 1
            sum = sum + v.value
            if v.value < lowest then
                lowest = v.value
            end
        end
    end
    local off_set = 1 - 0.7*(values_left/#game_values)
    local initial = lowest + (sum/values_left - lowest) * off_set
    local next_lower = -1
    for _, v in ipairs(game_values) do
        if v.in_play then
            if v.value > next_lower and v.value <= initial then
                next_lower = v.value
            end
        end
    end
    return math.floor(next_lower*(1-off_set) + initial*off_set)
end

This behaves more similarly to the banker in the TV show this is based on:

• early offers are further below the expected value of a case, later offers are much closer
• offers get "pulled towards" the next worst case; strength of this effect also declines as the game continues
• offers will never be worse than the lowest case on the board

Also, here's an improvement to draw_offer (adding a helper function, too) that reminds players how long the next round will be:

function pluralize_cases(n)
  if (n == 1) return "1 case"
  return tostr(n.." cases")
end

function draw_offer()
    if round == 7 then
        print("LAST OFFER", 56, 20, FONT_COLOR)
    else
        print("next round:\n   "..pluralize_cases(CASES_PER_ROUND[round+1]),
              100, 112)
    end
    print("Offer: $" .. comma_value(current_offer), 50, 30, FONT_COLOR)
    btn_deal:draw()
    btn_no_deal:draw()
    draw_display_values()
end

Finally, here's a better way to initialize game_values, iniside __init():

    game_values = {}
    for _, v in ipairs(CASE_VALUES) do
        add(game_values, {value=v, in_play = true})
    end

That way you can change just the values in the CASE_VALUES list and it will work -- you don't have to change it in two spots. I tinkered with this a bit to make the numbers work out more like the TV show by removing the $900K and $250K, and inserting $200K and $300K. I mention this because my algorithm seems to give strangely high offers at the start of the game with your money tree, but the numbers look much more familiar with the less generous payout table.

Edited to add: I've played around with this a bit more. I think the quadratic curve for using the offset in weighting between the initial estimate and the "next worse" case works better -- if you want to try that out, replace the last line in my proposed get_offer() with

return math.floor(next_lower*(1-off_set*off_set) + initial*off_set*off_set

and see how that feels for you!

Sorry to be rewriting your thing so aggressively, I have been having fun experimenting with different algorithms for making offers.

@Kistaro,

No need to apologize. Your improvements are greatly appreciated and have been implemented.