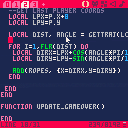
Heyo people! I've been learning Pico 8 for a few weeks now, created a few little test games to learn the language, now I'm trying to start a game I intend to finish and polish - thought it might be useful to start interacting on the boards. I'm having some issues with the mathematics of this game I'm making.
Playing as a small turtle with a cactus on it's back, the main mode of interaction will be snatching other entities out of the air with rope-like tendrils that come from within the cactus. However, right now, I'm having a lot of difficulty trying to figure out why my tendrils are not lining up to the angle of the mouse's location (using mouse input). Sine, cosine, pi, all that stuff terrifies me, so if someone out there wouldn't mind taking a gander at the small amount of code I've written for this project so far, I'd appreciate any advice!
Thanks!
The I suspect the problem lies somewhere here...
function gettraj(mx,my)
--get x/y distances
local hdist=p.x-(mx+4)
local vdist=p.y-(my+4)
--get diagonal distance
local dist=sqrt(hdist^2+vdist^2)
--get angle to cursor in degrees
local angle=(atan2(vdist,hdist)*180/pi)+45
return dist, angle
end
function update_game()
mousex=stat(32)
mousey=stat(33)
mousebtn=stat(34)
if band(mousebtn,1) > 0 then
--get last mouse coords
local lcursx=mousex
local lcursy=mousey
--get last player coords
local lpx=p.x+8
local lpy=p.y
local dist, angle = gettraj(lcursx,lcursy)
for i=1,flr(dist) do
local dirx=lpx+cos(angle*pi/180)*i
local diry=lpy-sin(angle*pi/180)*i
add(ropes, {x=dirx,y=diry})
end
end
end |

Hi @shabbycat, this is a good start!
You suspect correctly. Honestly you've got the right idea there are just a few little mistakes. The first is hdist and vdist. If you think of the player's position as the start point and the mouse position as the end point, you always want to calculate distances like this as: end_point - start_point. Otherwise your directions (and therefore ropes) end up reversed. Also when you calculate the trajectory you're using p.x but when you calculate the end point of your rope you're using p.x + 8 which will throw off where you expect it to be. Either is fine but they should both be the same.
--get x/y distances local hdist=mx - p.x - 4 -- equivalent to (mx+4) - (p.x+8) local vdist=(my+4) - p.y |
That's actually not happening to you because of the second problem: Your arguments to atan2 are reversed. I do that all the time and have to look it up almost every single time because I can never remember what order they're supposed to be in but it should be atan2(hdist, vdist).
About angles on pico-8. Angles are measured between 0 and 1. 360 degrees, one full turn, is just 1. 180 degrees, a half turn, is 0.5, etc. You're free to convert back and forth between degrees if you want to but you don't need to. So if you want to add 45 degrees to the angle, 45 degrees is 1/8 of a turn around the circle or 0.125. So you could just add 0.125 to the angle you get back from atan2.
I'm not sure why you're adding 45 degrees though. If you have a reason I'm just not aware of then feel free to ignore this advice but if you want the rope to line up with the mouse then all you need is this:
--get angle to cursor in degrees local angle=atan2(hdist,vdist) |
Similarly, since you don't need to convert back and forth between degrees your sin and cos calls can be simplified too.
for i=1,flr(dist) do
local dirx=lpx+cos(angle)*i
local diry=lpy+sin(angle)*i
add(ropes, {x=dirx,y=diry})
end |
This is another, "if you have a reason then just ignore me," situations. But you probably don't need the loop. You can just do this:
local dirx=lpx+cos(angle)*dist
local diry=lpy+sin(angle)*dist
add(ropes, {x=dirx,y=diry}) |
and then in your draw instead of circfill you can use line
for rope in all(ropes) do
line(p.x+8, p.y, rope.x, rope.y, 7)
end |
Putting all that together:
function gettraj(mx,my)
--get x/y distances
local hdist=mx - p.x - 4 -- equivalent to (mx+4) - (p.x+8)
local vdist=(my+4) - p.y
--get diagonal distance
local dist=sqrt(hdist^2+vdist^2)
--get angle to cursor in degrees
local angle=atan2(hdist,vdist)
return dist, angle
end
function update_game()
mousex=stat(32)
mousey=stat(33)
mousebtn=stat(34)
if band(mousebtn,1) > 0 then
--get last mouse coords
local lcursx=mousex
local lcursy=mousey
--get last player coords
local lpx=p.x+8
local lpy=p.y
local dist, angle = gettraj(lcursx,lcursy)
local dirx=lpx+cos(angle)*dist
local diry=lpy+sin(angle)*dist
add(ropes, {x=dirx,y=diry})
end
end
function draw_game()
cls(0)
map()
spr(p.sp,p.x,p.y,2,2,false)
spr(48,mousex,mousey)
for rope in all(ropes) do
line(p.x+8, p.y, rope.x, rope.y, 7)
end
end |
Hope that helps!

Hi @jasondelaat! Thanks so much for the detailed response, it was really useful.
The 45 degree angle addition was just an attempt to correct the angle macguiver style rather than trying to fix the root problem heh, so I really appreciate you helping me to understand what was going on. The 'line' addition definitely makes things simpler for now, but I do think I'll experiment with the loop a little more since I don't want the ropes to instantly reach their destination.
Just to confirm, the unconverted angle value is in radians, correct? I tried to convert to make it simpler for me to understand, but the way you explained it, it seems pretty straightforward. Saves on tokens too, so thanks!
I am a little concerned, as I'm still having trouble visualising what the code is doing step by step, but I think with time it should start to come to me.

> Just to confirm, the unconverted angle value is in radians, correct?
Actually no. In radians one full turn around the circle takes 2*pi (so approximately 6.28) radians. In case you're unsure about what exactly radians are, if you have a circle with radius r and walk around the edge of the circle so that you travel a distance of r, the angle that you get is 1 radian.
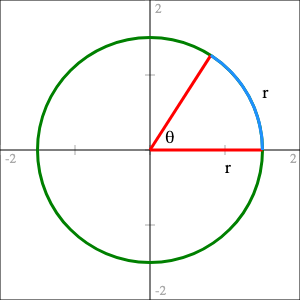
So if you straighten out that blue section it's the same length as one of the red arms. And you can fit just a little over 6 of those blue sections around the entire circle.
Pico-8's angles are just a percentage of a full turn: 0 is 0%, 0.5 is 50%, 1 is 100%, etc.

Ahhh, that's way simpler. Thanks for clarifying! Slowly I'm clawing my way back to elementary level math.
[Please log in to post a comment]