Log In  



Cart #vector_p8-12 | 2024-10-23 | Code ▽ | Embed ▽ | License: CC4-BY-NC-SA
14

vector.p8

a simple and lightweight (in tokens) vector math library for PICO-8.

usage:

  • load #vector_p8 and save as such: vector.p8
  • remove all the demo code; it's in the second tab
  • #include in any cart you want

functions within:

> NOTE:
> vectors are just normal Lua tables with x and y fields, so you can pass any table that contains x and y to any of the functions and they will work regardless.

creation and management

vector(x,y) - the main function. x and y default to 0

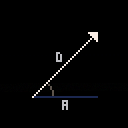
v_polar(angle, length) - makes a new vector using polar coordinates
v_rnd() - returns a normalized vector with a random direction

v_copy(v) - returns a copy of v
v_unpack(v) - returns the components of v separately
v_tostr(v) - turns a vector into a string, appropriate for both debugging and normal output. it looks like [x, y]

actual math

v_add(a,b) - returns a + b
v_sub(a,b) - returns a - b
v_scale(v,n) - returns v scaled by n
v_mul(v,n) - alias for v_scale
v_div(v,n) - returns v scaled by the inverse of n

v_dot(a,b) - returns the dot product of a and b
v_magsq(v) - returns the squared magnitude of v
v_mag(v) - returns the magnitude of v
v_distsq(a,b) - returns the squared distance between a and b
v_dist(a,b) - returns the distance between a and b
v_norm(v) - returns v, normalized

v_perp(v) - returns a vector clockwise-perpendicular to v
v_proj(a,b) - returns the projection of b onto a
v_dir(a,b) - returns a normalized vector that points towards b, with origin at a.

v_rot(v,t) - returns v rotated to point towards angle t.
v_rotby(v,t) - returns v rotated by t.
v_angle(v) - returns the angle denoted by v

miscellaneous

v_lerp(a,b,t) - linearly interpolates from a to b by t
v_flr(v) - returns v, with all its components floored

constants

> WARNING!
> because of the way Lua tables work, do NOT use compound assignments to alter a variable if you directly assign one of these constants to it. either copy the constant using v_cpy and then assign that to the variable or use one of the functions within the library to manipulate it.

v_right - rightwards pointing vector.
v_left - leftwards pointing vector.
v_up - upwards pointing vector. Y points downward in 2D so this vector points towards -Y.
v_down - downwards pointing vector. Y points downward in 2D so this vector points towards +Y.
v_one - identity vector. all components are set to 1.
v_center - utility vector pointing towards the center of the screen, i.e. [64,64].

changelog

format: dd-mm-yyyy

v2.3 (23-10-2024):

  • fixed v_lerp using v_scl instead of v_scale or v_mul
  • v_rot rotates to t, not by t; changed the docs of v_rot to mention that, and added v_rotby
  • post related update: removed the "rotation related functions" section; not exactly useful

v2.2 (02-10-2024):

  • fixed undefined global call to v_dstsq in v_dist (see v2.0 changelog)
  • added version number to cart title
  • programmed a new demo! check the second tab in the editor (tab 1)

v2.1.1 (02-10-2024):

  • accidentally switched x and y around in v_angle, sorry about that

v2.1 (02-10-2024):

  • the calls to cos and sin in v_polar were swapped with each other
  • the formula for v_proj was taken from Wikipedia, and it projects b onto a, not a onto b; the docs were updated to reflect that

v2.0 (24-05-2024):
almost a 50% reduction on tokens, in exchange for various breaking changes:

  • removed v_eq, v_zero, v_atwds, v_isvec, v_arr and v_sprj
  • removed z component from all functions, the 3D constants and v_cross
    as in, this library no longer supports 3D math. sorry. it was oddly shoehorned in though, so I really wouldn't have relied on it that much.
  • added v_dir, taken from a mod of the library done by snale
  • optimized v_lerp, v_sub and v_rot
  • v_proj now uses the proper definition for vector projection
  • extended the names of some functions:
    • v_cpy -> v_copy
    • v_unpck -> v_unpack
    • v_scl -> v_scale
    • v_ang -> v_angle
    • v_cntr -> v_center
    • v_dst -> v_dist
    • v_dstsq -> v_distsq

v1.2.1 (11-03-2023):

  • thought I had fixed all functions that used v_getd, but turns out one function I hadn't added to the docs, v_flr, still used it
  • documented v_flr
  • improved explanation for v_atwds

v1.2 (06-12-2022):

  • fixed the math functions v_add, v_sub, v_scl, v_div and v_neg using the now-defunct v_getd function

v1.1 (09-11-2022):

  • removed all dimension related functions
    Consequently, a parameter was added to v_tostr for it to know how to format the output
  • added v_sprj and v_proj
  • renamed v_center to v_cntr

v1.0 (09-11-2022):

  • initial release
14

i got an error loading it up

oh yeah, right, the cart here has a demo, you gotta remove that code and then you can use the lib. I gotta put that in the post...
1

Excellent! Thank you for sharing.
1

This is great, thank you!

Two questions:

  1. v_polar seems to invert x and y, shouldn't it be x=l*cos(a) and y=l*sin(a)?
  2. from my experiments, it looks like v_proj is projecting b on a, instead of a on b (as stated in the description)

It's been a while since I studied trig, so I may have gotten both completely wrong :)
1

funnily enough, you're right on both :)

v_polar is like that because when I wrote this library I wasn't aware sin and cos weren't interchangeable, so I used them in either order, and I guess I just forgot about it

and for v_proj, I guess I'll just swap a and b in the description

I'll push a single minor update to fix both of these, thanks for pointing out both errors!

whoops sorry I pushed 3, my bad

I'm using your lib in my game and it's saving me a lot of time.

Hope you don't mind if I keep posting minor issues as I find them, sorry in advance for the spam:

  • v_lerp calls v_scl instead of v_scale

I also added three functions that I needed, feel free to add them if you like'em

 
function v_limit(v,n)
	local mgsq=v_magsq(v)
	if mgsq > n*n then
		return v_scale(v_div(v,sqrt(mgsq)),n)
	end
	return v	
end

function v_bounce(v,n,br)
	--https://gamedev.stackexchange.com/a/35537
	return	v_sub(v,v_mul(n,(1+br)*v_dot(v,n)))
end
v_reflect=v_bounce

function v_grow(v,n)
	local vm=v_mag(v)
	local norm=v_div(v,vm)
	return v_mul(norm,vm+n)
end


oop, didn't catch that one either, thanks!

about the extra functions:

  • v_bounce is the vector reflection function, would be better if you called it v_reflect
  • v_grow could be left off as it can be replicated in this way: 
    local m = v_mag(v)
local g = v_scale(v, (m+n)/m)

    but it does look more intuitive as a function

  • v_limit also sounds useful, but it's the kinda function you'd rather implement in code than in the library, though I'm probably biased

that being said, I'm not sure whether to add those functions... maybe if they're really commonly used but I don't usually check that kinda stuff

also again, thanks for reporting that bug, just released a patch version



[Please log in to post a comment]